
【题目】已知一次函数y=ax+b过一,二,四象限,且过(6,0),则关于二次函数y=ax2+bx+1的以下说法:①图象与x轴有两个交点;②a<0,b>0;③当x=3时函数有最小值;④若存在一个实数m,当x≤m时,y随x的增大而增大,则m≤3.其中正确的是( )
A. ①②B. ①②③C. ①②④D. ②③④
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“金山银山,不如绿水青山”.鄂尔多斯市某旗区不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题:
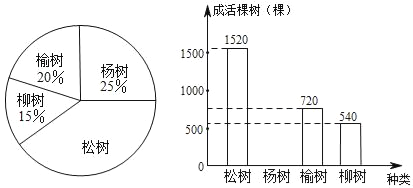
(1)扇形统计图中松树所对的圆心角为 度,并补全条形统计图.
(2)该旗区今年共种树32万棵,成活了约多少棵?
(3)园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a<0;④b2+8a>4ac,其中正确的有( )
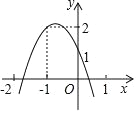
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
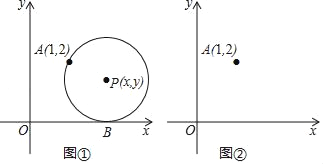
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)当x=2时,求⊙P的半径;
(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BD,CF⊥BD,E,F分别为垂足.
(1)求证:四边形AECF是平行四边形;
(2)如果AE=3,EF=4,求AF、EC所在直线的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
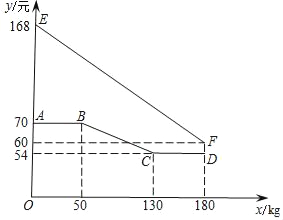
【题目】绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.
(1)求该产品销售价y1(元)与产量x(kg)之间的函数关系式;
(2)直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(提出问题)如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.
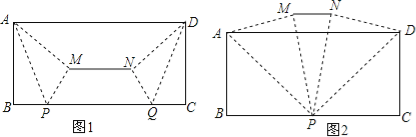
(规律探索)
(1)请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
(解决问题)
(2)如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
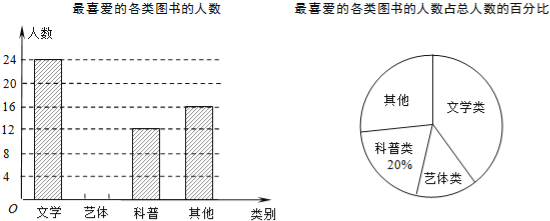
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() (点
(点![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ),射线
),射线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() .
.
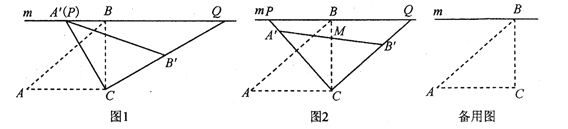
(1)如图1,当![]() 与
与![]() 重合时,求
重合时,求![]() 的度数;
的度数;
(2)如图2,设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 为
为![]() 的中点时,求线段
的中点时,求线段![]() 的长;
的长;
(3)在旋转过程中,当点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值.若存在,求出四边形
的面积是否存在最小值.若存在,求出四边形![]() 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com