
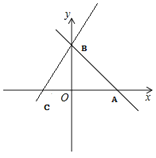
【题目】已知:如图,在平面直角坐标系中,直线y=-x+6与x轴、y轴分别交于A、B两点、
直线y=![]() ax+a经过点B交x轴于点C.
ax+a经过点B交x轴于点C.
(1)求AC长;
(2)点D为线段BC上一动点,过点D作x轴平行线分别交OB、AB于点E、F,点G为AF中点,直线EG交x轴于H,设点D的横坐标为t,线段AH长为d(d≠0),求d与t之间的函数关系式;
(3)在(2)的条件下,点K为线段OA上一点,连接EK,过F作FM⊥EK,直线FM交x轴于点M,当KH=2CO,点0到直线FM的距离为![]() 时,求点D的坐标。
时,求点D的坐标。


备用图 备用图
【答案】(1)AC长是9 ;(2)d=-2t ;(3)D![]() ,
, ![]()
【解析】试题分析:(1)令y=0时,可得到A、C的坐标,从而得到答案;
(2)先直线BC解析式为y=2x+6.表示出![]() ,进一步得到x=-2t.再证明ΔEFG≌ΔHAG,得到AH=EF=-2t .
,进一步得到x=-2t.再证明ΔEFG≌ΔHAG,得到AH=EF=-2t .
(3)过A点作PA⊥AC交DF的延长线于R,交MF的延长线于P,作ON⊥FM于N,PM交EK于点Q,则四边形OARE是矩形,可证ΔEKO≌ΔFPR,得到PR=OK=-2t.设OM=m,PA=2t+6-2t=6.分两种情况讨论:①当M点在x轴的负半轴上时,②当M点在x轴的正半轴上时.
试题解析:解:(1)当y=0时,-x+6=0,∴x=6,∴A(6,0) , ![]() ax+a=0,∴a(
ax+a=0,∴a(![]() x+1)=0.∵a≠0,∴
x+1)=0.∵a≠0,∴![]() x+1=0,∴x=-3 ,C(-3,0),∴AC=6-(-3)=9,∴AC长是9.
x+1=0,∴x=-3 ,C(-3,0),∴AC=6-(-3)=9,∴AC长是9.
(2)当x=0时,y=6,∴B(0,6),∴a=6,∴直线BC解析式为y=2x+6.
当x=t时, ![]() .∵DF∥AC,
.∵DF∥AC, ![]() ,∴2t+6=-x+6,∴x=-2t,∴EF=-2t,
,∴2t+6=-x+6,∴x=-2t,∴EF=-2t,
∵点G为AF中点,∴AG=GF .∵DF∥AC,∴∠FEG=∠GHA,∠EGF=∠HGA,∴ΔEFG≌ΔHAG,∴AH=EF=-2t .
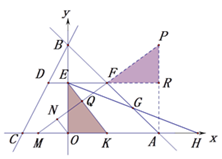
(3)过A点作PA⊥AC交DF的延长线于R,交MF的延长线于P,作ON⊥FM于N,PM交EK于点Q,四边形OARE是矩形,∴ER=OA=6,∴FR=2t+6=OE,可证∠P=∠KEO,∠PRE=∠EOK=90°,∴ΔEKO≌ΔFPR,∴PR=OK.∵KH=2CO=2×3=6,∴PR=OK=-2t.
设OM=m,PA=2t+6-2t=6.分两种情况讨论:
①M点在x轴的负半轴上时.∵![]() ,sin∠NMO=
,sin∠NMO=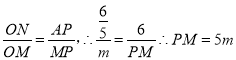 ,AM=m+6,由勾股定理可求:m1=
,AM=m+6,由勾股定理可求:m1=![]() (不合题意舍去),m2=2,tan∠PMA=
(不合题意舍去),m2=2,tan∠PMA=![]()
![]() .
.
②M点在x轴的正半轴上时,AM=6-m与同理可求:m1=![]() (不合题意舍去),m2=
(不合题意舍去),m2=![]() ,
,
tan∠PMA=![]()
![]() .
.
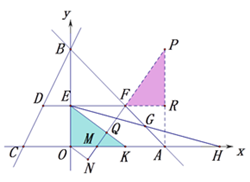


科目:初中数学 来源: 题型:
【题目】有一水果店,从批发市场按4元![]() 千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨
千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨![]() 元.
元.
![]() 设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
![]() 若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
![]() 该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点A(-3,4).
经过点A(-3,4).
(1)求b的值;
(2)过点A作![]() 轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
①当点C恰巧落在![]() 轴时,求直线OP的表达式;
轴时,求直线OP的表达式;
②连结BC,求BC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲于某日下午1时骑自行车从A地出发前往B地,乙于同日下午骑摩托车从A地出发前往B地,如图所示,图中折线PQR和线段MN分别表示甲和乙所行驶的路程和时间之间的关系图象,试根据图象回答下列问题.
(1)A、B两地相距多少千米?甲出发几小时,乙才开始出发?
(2)甲骑自行车的平均速度是多少?乙骑摩托车的平均速度是多少?
(3)乙在该日下午几时追上了甲?这时两人离B地还有多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,若AB∥CD,求∠B+∠D+∠E1的度数?
(2)如图②,若AB∥CD,求∠B+∠D+∠E1+∠E2的度数?
(3)如图③,若AB∥CD,求∠B+∠D+∠E1+∠E2+∠E3的度数?
(4)如图④,若AB∥CD,猜想∠B+∠D+∠E1+∠E2+…+∠En的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[x]表示不超过x的最大整数,例如[﹣3.5]=﹣4,[2.1]=2,若y=x﹣[x],下列命题:①当x=﹣0.5时,y=0.5;②y的取值范围是:0≤y≤1;③对于所有的自变量x,函数值y随着x增大而一直增大.其中正确命题有 (只填写正确命题的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三角形的两条边长为1cm和2cm,一个内角为45°.
(1)请你利用如图45°角,画出一个满足题设条件的三角形.
(2)你是否还能画出既满足题设条件,又与(1)中所画的不全等的三角形?若能,请用“尺规作图”画出,若不能,请说明理由.
(3)如果将题设条件改为“一个三角形的两条边长为3cm和4cm,一个内角为45°”,画出满足这一条件的,且彼此不全等的所有三角形.(要求在图中标记3cm和4cm的边长)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是-块长方形空地,长为![]() 米,宽为
米,宽为![]() 米,现要对其进行修整,在空白部分铺设
米,现要对其进行修整,在空白部分铺设![]() 条宽度为
条宽度为![]() 米的小路,其余阴影部分种植草坪.
米的小路,其余阴影部分种植草坪.

(1)用整式表示小路的面积;
(2)用整式表示草坪的面积;
(3)现有两种修整方案,方案一:修建小路的宽度为![]() 米;方案二:修建小路的宽度为
米;方案二:修建小路的宽度为![]() 米.铺设小路的造价为每平方米
米.铺设小路的造价为每平方米![]() 元,种植草坪的造价为每平方米
元,种植草坪的造价为每平方米![]() 元,请问选用哪种方案最划算.( 写出计算过程)
元,请问选用哪种方案最划算.( 写出计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com