
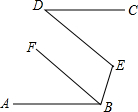
 如图,AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠D的关系是∠ABE=2∠D.
如图,AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠D的关系是∠ABE=2∠D.  学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
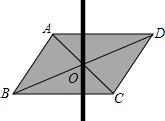 如图,用硬纸板剪一个平行四边形,作出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,使它随意停留在任意位置,观察几次拨动的结果,你发现了什么?证明你的发现.
如图,用硬纸板剪一个平行四边形,作出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,使它随意停留在任意位置,观察几次拨动的结果,你发现了什么?证明你的发现.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com