
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 x+1,
x+1, (2)x<-2或0<x<4
(2)x<-2或0<x<4 的图象与y轴交于点A,与x轴交于点B,
的图象与y轴交于点A,与x轴交于点B,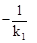 ,0)。
,0)。 ×OB×OA=1,即
×OB×OA=1,即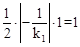 。∴
。∴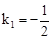 。
。 x+1。
x+1。 x+1=2,解得x=-2。∴M的坐标为(-2,2)
x+1=2,解得x=-2。∴M的坐标为(-2,2) 。
。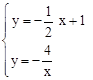 得
得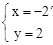 或
或 ,
,

科目:初中数学 来源:不详 题型:解答题
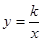 和
和
 的图像关于
的图像关于 轴对称,我们把函数
轴对称,我们把函数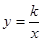 和
和
 叫做互为“镜子”函数.类似地,如果函数
叫做互为“镜子”函数.类似地,如果函数 和
和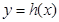 的图像关于
的图像关于 轴对称,那么我们就把函数
轴对称,那么我们就把函数 和
和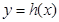 叫做互为“镜子”函数.
叫做互为“镜子”函数.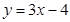 的“镜子”函数: ,(3分)
的“镜子”函数: ,(3分)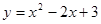 ; (3分)
; (3分) (
(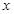 >
>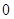 )和
)和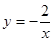 (
(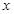 <
<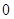 )的图像分别交于点
)的图像分别交于点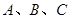 ,如果
,如果 ,点
,点 在函数
在函数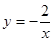 (
(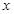 <
<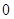 )的“镜子”函数上的对应点的横坐标是
)的“镜子”函数上的对应点的横坐标是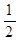 ,求点
,求点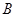 的坐标. (6分)
的坐标. (6分)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
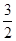 ),过点P作x轴的平行线交y轴于点A,交双曲线
),过点P作x轴的平行线交y轴于点A,交双曲线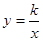 (x>0)于点N;作PM⊥AN交双曲线
(x>0)于点N;作PM⊥AN交双曲线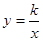 (x>0)于点M,连结AM.已知PN=4.
(x>0)于点M,连结AM.已知PN=4.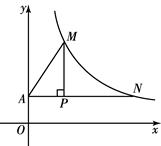
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象上,且
的图象上,且| A.y3<y1<y2 | B.y1<y2<y3 | C.y3<y2<y1 | D.y2<y1<y3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com