
【题目】在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、9时,△ABC为 三角形;当△ABC三边分别为6、8、11时,△ABC为 三角形.
(2)猜想,当a2+b2 c2时,△ABC为锐角三角形;当a2+b2 c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
【答案】解:(1)锐角;钝角。
(2)>;<。
(3)①当4≤c<2![]() 时,这个三角形是锐角三角形;
时,这个三角形是锐角三角形;
②当c=2![]() 时,这个三角形是直角三角形;
时,这个三角形是直角三角形;
③当2![]() <c<6时,这个三角形是钝角三角形.。
<c<6时,这个三角形是钝角三角形.。
【解析】
试题分析:(1)利用勾股定理列式求出两直角边为6、8时的斜边的值,然后作出判断即可:
∵两直角边分别为6、8时,斜边=10,
∴当△ABC三边分别为6、8、9时,△ABC为锐角三角形;
当△ABC三边分别为6、8、11时,△ABC为钝角三角形。
(2)根据(1)中的计算作出判断即可;
当a2+b2>c2时,△ABC为锐角三角形;当a2+b2<c2时,△ABC为钝角三角形。
(3)根据三角形的任意两边之和大于第三边求出最长边c点的最大值,然后得到c的取值范围,然后分情况讨论即可得解。
∵c为最长边,2+4=6,∴4≤c<6,a2+b2=22+42=20。
①a2+b2>c2,即c2<20,0<c<2![]() ,
,
∴当4≤c<2![]() 时,这个三角形是锐角三角形;
时,这个三角形是锐角三角形;
②a2+b2=c2,即c2=20,c=2![]() ,
,
∴当c=2![]() 时,这个三角形是直角三角形;
时,这个三角形是直角三角形;
③a2+b2<c2,即c2>20,c>2![]() ,
,
∴当2![]() <c<6时,这个三角形是钝角三角形.
<c<6时,这个三角形是钝角三角形.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】有以下说法:其中正确的说法有( )
(1)开方开不尽的数是无理数;
(2)无理数是无限循环小数
(3)无理数包括正无理数和负无理数;
(4)无理数都可以用数轴上的点来表示;
(5)循环小数都是有理数
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
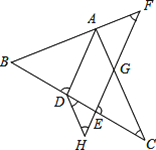
【题目】如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,则∠F与∠H相等吗,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照题中提供的思路点拨,先填空,然后完成解答的全过程.
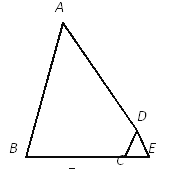
如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨:(1)由已知条件AB=AD,∠BAD=60°,可知△ABD是_三角形.同理由已知条件∠BCD=120°得到∠DCE=_,且CE=CD,可知_;
(2)要证BC+DC=AC,可将问题转化为证两条线段相等,即_=_;
(3)要证(2)中所填写的两条线段相等,可以先证明_.请写出完整的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为鼓励失地农民自主创业,在2010年对60位自主创业的失地农民进行了奖励,共计奖励了10万元.奖励标准是:失地农民自主创业连续经营一年以上的给予1000元奖励:自主创业且解决5人以上失业人员稳定就业一年以上的,再给予2000元奖励.问:该县失地农民中自主创业连续经营一年以上的和自主创业且解决5人以上失业人员稳定就业一年以上的农民分别有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com