
【题目】已知一次函数![]() ,当
,当![]() 时,
时,![]() ,则此函数与
,则此函数与![]() 轴的交点坐标是__________.
轴的交点坐标是__________.
【答案】(0,![]() )或(0,
)或(0,![]() )
)
【解析】
根据k的取值分类讨论,①当k>0时,y随x增大而增大,可知一次函数过![]() 两点,利用待定系数法求出一次函数的解析式,然后将x=0代入即可求出此函数与
两点,利用待定系数法求出一次函数的解析式,然后将x=0代入即可求出此函数与![]() 轴的交点坐标;②当k<0时,y随x增大而减小,可知一次函数过
轴的交点坐标;②当k<0时,y随x增大而减小,可知一次函数过![]() 两点,利用待定系数法求出一次函数的解析式,然后将x=0代入即可求出此函数与
两点,利用待定系数法求出一次函数的解析式,然后将x=0代入即可求出此函数与![]() 轴的交点坐标.
轴的交点坐标.
解:①当k>0时,y随x增大而增大
∵当![]() 时,
时,![]()
∴一次函数过![]() 两点
两点
将![]() 代入解析式中,得
代入解析式中,得
![]()
解得:
故该一次函数的解析式为![]()
将x=0代入,解得y=![]() ,
,
故此函数与![]() 轴的交点坐标是(0,
轴的交点坐标是(0,![]() );
);
②当k<0时,y随x增大而减小
∵当![]() 时,
时,![]()
∴一次函数过![]() 两点
两点
将![]() 代入解析式中,得
代入解析式中,得
![]()
解得: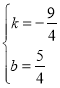
故该一次函数的解析式为![]()
将x=0代入,解得y=![]() ,
,
故此函数与![]() 轴的交点坐标是(0,
轴的交点坐标是(0,![]() );
);
综上所述:此函数与![]() 轴的交点坐标是(0,
轴的交点坐标是(0,![]() )或(0,
)或(0,![]() )
)
故答案为:(0,![]() )或(0,
)或(0,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB、AD中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=( )

A.1.2 里B.1.5 里C.1.05 里D.1.02 里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数![]() 和
和![]() 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥
的图象上,PC⊥![]() 轴于点C,交
轴于点C,交![]() 的图象于点A,PC⊥
的图象于点A,PC⊥![]() 轴于点D,交
轴于点D,交![]() 的图象于点B. 当点P在
的图象于点B. 当点P在![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①![]()
②![]() 的值不会发生变化
的值不会发生变化
③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=40°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
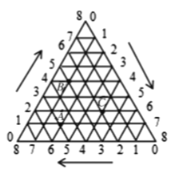
【题目】如图,将一等边三角形的三条边各8等分,按顺时针方向(图中箭头方向)标注各等分点的序号0、1、2、3、4、5、6、7、8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系.在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点![]() 的坐标可表示为(1,2,5),点
的坐标可表示为(1,2,5),点![]() 的坐标可表示为(4,1,3),按此方法,则点
的坐标可表示为(4,1,3),按此方法,则点![]() 的坐标可表示为( )
的坐标可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD.BC上,且DE=BP=1.连接BE,EC,AP,DP,PD与CE交于点F,AP与BE交于点H.
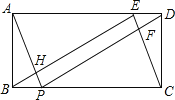
(1)判断△BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形,并证明你的判断;
(3)求四边形EFPH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
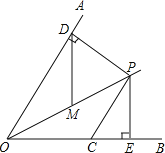
【题目】如图,已知 OP 平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com