
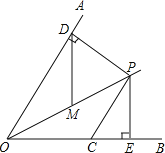
【题目】如图,已知 OP 平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是_________.
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】知识背景
我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定,在十三章《轴对称》中学习了等腰三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题

问题初探
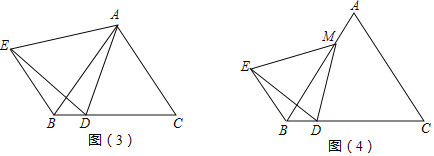
如图(1),△ABC中,∠BAC=90°,AB=AC,点D是BC上一点,连接AD,以AD为一边作△ADE,使∠DAE=90°,AD=AE,连接BE,猜想BE和CD有怎样的数量关系,并说明理由.
类比再探
如图(2),△ABC中,∠BAC=90°,AB=AC,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作△MDE,使∠DME=90°,MD=ME,连接BE,则∠EBD= .(直接写出答案,不写过程,但要求作出辅助线)
方法迁移
如图(3),△ABC是等边三角形,点D是BC上一点,连接AD,以AD为一边作等边三角形ADE,连接BE,则BD、BE、BC之间有怎样的数量关系? (直接写出答案,不写过程).
拓展创新
如图(4),△ABC是等边三角形,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作等边三角形MDE,连接BE.猜想∠EBD的度数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
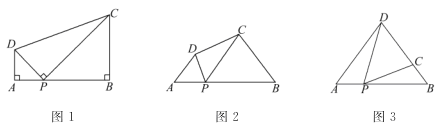
【题目】(1)、问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证:AD·BC=AP·BP.
(2)、探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)、应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A 出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当DC的长与△ABD底边上的高相等时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
方案二:购买门票方式如图所示.
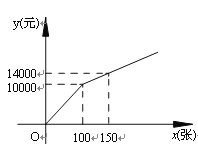
解答下列问题:
(1)方案一中,y与x的函数关系式为 ;
方案二中,当0≤x≤100时,y与x的函数关系式为 ,当x>100时,y与x的函数关系式为 ;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,则下列条件中不一定能使△ABC≌△ABD的是( )

A. AC=AD B. BC=BD C. ∠C=∠D D. ∠3=∠4
查看答案和解析>>
科目:初中数学 来源: 题型:
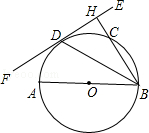
【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com