
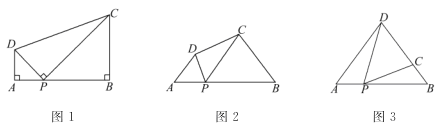
����Ŀ��(1)�����⣺��ͼ1�����ı���ABCD�У���PΪAB��һ�㣬��DPC=��A=��B=90������֤��AD��BC=AP��BP��
(2)��̽������ͼ2�����ı���ABCD�У���PΪAB��һ�㣬����DPC=��A=��B=��ʱ�����������Ƿ���Ȼ������˵�����ɣ�
(3)��Ӧ�ã������ã�1����2����õľ��������⣺
��ͼ3������ABD�У�AB=6��AD=BD=5����P��ÿ��1����λ���ȵ��ٶȣ��ɵ�A �������ر�AB���B�˶����������DPC=��A�����P���˶�ʱ��Ϊt���룩����DC�ij�����ABD�ױ��ϵĸ����ʱ����t��ֵ��
���𰸡���1��֤������������2�����۳���. (3)��t=1���5��.
�����������⣨1������DPC=��A=��B=90���ɵ���ADP=��BPC������֤����ADP�ס�BPC��Ȼ���������������ε����ʼ��ɽ�����⣻
��2������DPC=��A=��B=���ɵ���ADP=��BPC������֤����ADP�ס�BPC��Ȼ���������������ε����ʼ��ɽ�����⣻
��3������D��DE��AB�ڵ�E�����ݵ��������ε����ʿɵ�AE=BE=6�����ݹ��ɶ����ɵ�DE=8������ɵ�DC=DE=8������BC=10-8=2����֤��DPC=��A=��B������AD![]() BC=AP
BC=AP![]() BP���Ϳ����t��ֵ��
BP���Ϳ����t��ֵ��
�����������1����ͼ1��
�ߡ�DPC=��A=��B=90����
���ADP+��APD=90����
��BPC+��APD=90����
���APD=��BPC��
���ADP�ס�BPC��
��![]() ��
��
��AD![]() BC=AP
BC=AP![]() BP��
BP��
��2������AD![]() BC=AP
BC=AP![]() BP�Գ�����
BP�Գ�����
֤������ͼ2���ߡ�BPD=��DPC+��BPC��
���ߡ�BPD=��A+��APD��
���DPC+��BPC=��A+��APD��
�ߡ�DPC=��A=����
���BPC=��APD��
���ߡ�A=��B=����
���ADP�ס�BPC��
��![]() ��
��
��AD![]() BC=AP
BC=AP![]() BP��
BP��
��3������ͼ������D��DE��AB�ڵ�E��
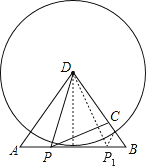
��AD=BD=10��AB=12��
��AE=BE=6
��DE=![]() =8��
=8��
����DΪԲ�ģ���DCΪ�뾶��Բ��AB���У�
��DC=DE=8��
��BC=10-8=2��
��AD=BD��
���A=��B��
���ߡ�DPC=��A��
���DPC=��A=��B��
�ɣ�1����2���ľ����ADBC=APBP��
����AP=t��BP=12-t��
��t��12-t��=10��2��
��t=2��t=10��
��t��ֵΪ2���10�룮


 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д� �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������![]() ��
��![]() �ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��
�ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��![]() ��ͼ���ϣ�PC��
��ͼ���ϣ�PC��![]() ���ڵ�C����
���ڵ�C����![]() ��ͼ���ڵ�A��PC��
��ͼ���ڵ�A��PC��![]() ���ڵ�D����
���ڵ�D����![]() ��ͼ���ڵ�B. ����P��
��ͼ���ڵ�B. ����P��![]() ��ͼ�����˶�ʱ�����½��ۣ�
��ͼ�����˶�ʱ�����½��ۣ�
��![]()
��![]() ��ֵ���ᷢ���仯
��ֵ���ᷢ���仯
��PA��PBʼ�����
�ܵ���A��PC���е�ʱ����Bһ����PD���е�.
����һ������ȷ����( )

A. �� B. �� C. �� D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=2,BC=5,E��P�ֱ���AD.BC�ϣ���DE=BP=1.����BE,EC,AP,DP,PD��CE���ڵ�F,AP��BE���ڵ�H��
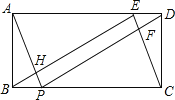
(1)�ж���BEC����״����˵�����ɣ�
(2)�ж��ı���EFPH��ʲô�����ı��Σ���֤������жϣ�
(3)���ı���EFPH�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯һ������Կ������ڱ�У���������������ѧ����������ÿ����ϲ���������˶�������ͳ�ƣ���������ͼ1��ͼ2��ʾ�����κ�����ͳ��ͼ��
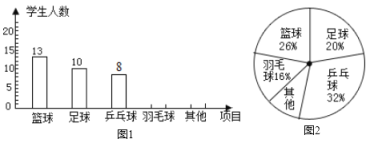
����ͳ��ͼ�е���Ϣ������������⣺
��1���α������ѧ������������ȫ����ͳ��ͼ��
��2����ȫУ��1500��ѧ����������Ƹ�У��ϲ�������˶���ѧ��������
��3�����ݵ�����������ΪѧУ������֯��һ���������������������飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���BAC=60�㣬��BAC��ƽ����AD���BC�Ĵ�ֱƽ�����ཻ�ڵ�D��DE��AB��AB���ӳ����ڵ�E��DF��AC�ڵ�F���������н��ۣ���DE=DF����DE+DF=AD����AMƽ�֡�ADF����AB+AC=2AE��������ȷ���У� ��

A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
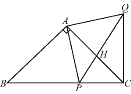
����Ŀ����ͼ������ABC����AB=AC����BAC=90�㣬��P��BC�ϵ�һ������AP=AQ����PAQ=90�㣬����CQ��
(1)��֤��CQ��BC��
(2)��ACQ�ܷ���ֱ������������������ֱ��д����ʱ��P��λ�ã�����������˵������.
(3)����P��BC��ʲôλ��ʱ����ACQ�ǵ�������������˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
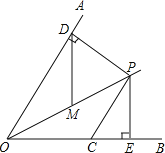
����Ŀ����ͼ����֪ OP ƽ�֡�AOB����AOB=60�㣬CP=2��CP��OA��PD��OA�ڵ�D��PE��OB�ڵ�E�������M��OP���е㣬��DM�ij���_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
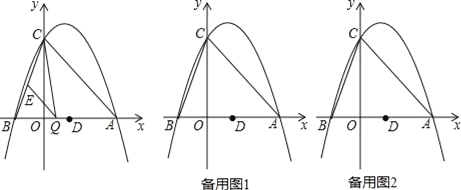
����Ŀ����ͼ��������y=ax2��2ax+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A����Ϊ��4��0����
��1����������ߵĽ���ʽ��
��2�������ߵĶ���ΪN����x������һ��K��ʹCK+KN��С���������K�����ꣻ
��3����Q���߶�AB�ϵĶ��㣬����Q��QE��AC����BC�ڵ�E������CQ������CQE��������ʱ�����Q�����ꣻ
��4����ƽ����x��Ķ�ֱ��l��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0�����ʣ��Ƿ����������ֱ��l��ʹ�á�ODF�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
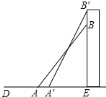
����Ŀ��һ����ͳ�![]() �ף�����
�ף�����![]() ��ǽ���ã���ˮƽ�н�Ϊ
��ǽ���ã���ˮƽ�н�Ϊ![]() ��Ϊ�˼���ռ�ؿռ䣬�ֽ������
��Ϊ�˼���ռ�ؿռ䣬�ֽ������![]() ���ã���ˮƽ�н�Ϊ
���ã���ˮƽ�н�Ϊ![]() ��������ó�����ˮƽ�ռ䣨 ��
��������ó�����ˮƽ�ռ䣨 ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com