
【题目】如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD.BC上,且DE=BP=1.连接BE,EC,AP,DP,PD与CE交于点F,AP与BE交于点H.
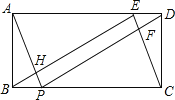
(1)判断△BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形,并证明你的判断;
(3)求四边形EFPH的面积.
【答案】(1)△BEC为直角三角形,理由见解析;(2)四边形EFPH是矩形,理由见解析;(3)![]()
【解析】
(1)根据矩形的性质可得∠BAE=∠CDE=90°,AB=CD=2,AD=BC=5,然后利用勾股定理即可求出BE和CE,然后根据勾股定理的逆定理即可证出△BEC为直角三角形;
(2)根据矩形的性质可得AD∥BC, AD=BC=5,然后根据平行四边形的判定定理可得四边形EBPD和四边形APCE均为平行四边形,从而证出四边形EFPH是平行四边形,然后根据矩形的定义即可得出结论;
(3)先利用三角形面积的两种求法,即可求出BH,从而求出HE,然后根据勾股定理即可求出HP,然后根据矩形的面积公式计算即可.
解:(1)△BEC为直角三角形,理由如下
∵四边形ABCD为矩形
∴∠BAE=∠CDE=90°,AB=CD=2,AD=BC=5
∵DE=1
∴AE=AD-DE=4
在Rt△ABE中,BE=![]()
在Rt△CDE中CE=![]()
∴BE2+CE2=25= BC2
∴△BEC为直角三角形
(2)四边形EFPH是矩形,理由如下
∵四边形ABCD为矩形
∴AD∥BC, AD=BC=5
∵DE=BP=1,
∴AD-DE=BC-BP=4
即AE=CP=4
∴四边形EBPD和四边形APCE均为平行四边形
∴EB∥DP,AP∥EC
∴四边形EFPH是平行四边形
∵△BEC为直角三角形,∠BEC=90°
∴四边形EFPH是矩形
(3)∵四边形APCE为平行四边形,四边形EFPH是矩形
∴AP=CE=![]() ,∠EHP=90°
,∠EHP=90°
∴∠BHP=180°-∠EHP=90°
∵S△ABP=![]()
∴![]()
解得:![]()
∴HE=BE-BH=![]()
在Rt△BHP中,HP =![]()
∴S矩形EFPH= HP·HE=![]()


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】近期江苏省各地均发布“雾霾”黄色预警,我市某口罩厂商生产一种新型口罩产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系满足下表.
销售单价x(元/件) | … | 20 | 25 | 30 | 40 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 20 | … |
(1)请你从所学过的一次函数、二次函数和反比例函数三个模型中确定哪种函数能比较恰当地表示y与x的变化规律,并直接写出y与x之间的函数关系式为__________;
(2)当销售单价为多少元时,厂商每月获得的利润为440万元?
(3)如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一条道路上,甲车从![]() 地到
地到![]() 地,乙车从
地,乙车从![]() 地到
地到![]() 地,乙先出发,图中的折线段表示甲、乙两车之间的距离
地,乙先出发,图中的折线段表示甲、乙两车之间的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)的函数关系的图象,根据图象解决以下问题:
(小时)的函数关系的图象,根据图象解决以下问题:
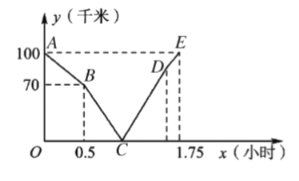
(1)乙先出发的时间为 小时,乙车的速度为 千米/时;
(2)求线段![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)甲、乙两车谁先到终点,先到多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.
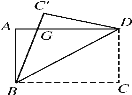
(1)求证:AG=C′G;
(2) 求△BDG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣x+1与抛物线y=![]() x2+bx+c交于A(0,1),B两点,B点纵坐标为10,抛物线的顶点为C.
x2+bx+c交于A(0,1),B两点,B点纵坐标为10,抛物线的顶点为C.
(1)求b,c的值;
(2)判断△ABC的形状并说明理由;
(3)点D、E分别为线段AB、BC上任意一点,连接CD,取CD的中点F,连接AF,EF.当四边形ADEF为平行四边形时,求平行四边形ADEF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识背景
我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定,在十三章《轴对称》中学习了等腰三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题

问题初探
如图(1),△ABC中,∠BAC=90°,AB=AC,点D是BC上一点,连接AD,以AD为一边作△ADE,使∠DAE=90°,AD=AE,连接BE,猜想BE和CD有怎样的数量关系,并说明理由.
类比再探
如图(2),△ABC中,∠BAC=90°,AB=AC,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作△MDE,使∠DME=90°,MD=ME,连接BE,则∠EBD= .(直接写出答案,不写过程,但要求作出辅助线)
方法迁移
如图(3),△ABC是等边三角形,点D是BC上一点,连接AD,以AD为一边作等边三角形ADE,连接BE,则BD、BE、BC之间有怎样的数量关系? (直接写出答案,不写过程).
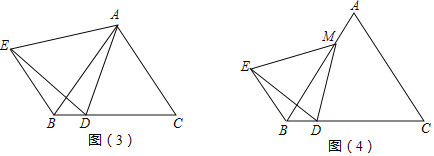
拓展创新
如图(4),△ABC是等边三角形,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作等边三角形MDE,连接BE.猜想∠EBD的度数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
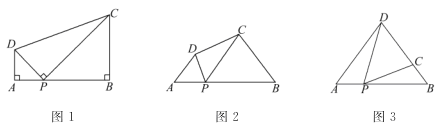
【题目】(1)、问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证:AD·BC=AP·BP.
(2)、探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)、应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A 出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当DC的长与△ABD底边上的高相等时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
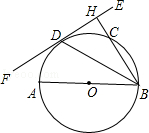
【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com