
【题目】如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.
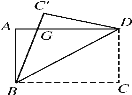
(1)求证:AG=C′G;
(2) 求△BDG的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据矩形的性质可得AD=BC,AB=DC,AD∥BC,∠BAD=90°,从而得出∠GDB=∠DBC,然后根据折叠的性质可得BC= BC′,∠GBD=∠DBC,从而得出AD= BC′,∠GBD=∠GDB,然后根据等角对等边可得GD=GB,即可证出结论;
(2)设GD=GB=x,利用勾股定理列出方程即可求出GD的长,然后根据三角形的面积公式求面积即可.
(1)证明:∵四边形ABCD为矩形
∴AD=BC,AB=DC,AD∥BC,∠BAD=90°
∴∠GDB=∠DBC
由折叠的性质可得BC= BC′,∠GBD=∠DBC
∴AD= BC′,∠GBD=∠GDB
∴GD=GB
∴AD-GD= BC′-GB
∴AG=C′G;
(2)解:设GD=GB=x,则AG=AD-GD=8-x
在Rt△ABG中![]()
即![]()
解得:![]()
即![]()
∴S△BDG=![]()


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”,
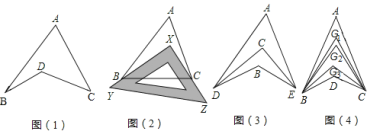
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX等于多少度;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
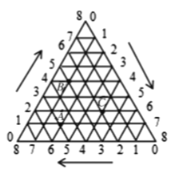
【题目】如图,将一等边三角形的三条边各8等分,按顺时针方向(图中箭头方向)标注各等分点的序号0、1、2、3、4、5、6、7、8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系.在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点![]() 的坐标可表示为(1,2,5),点
的坐标可表示为(1,2,5),点![]() 的坐标可表示为(4,1,3),按此方法,则点
的坐标可表示为(4,1,3),按此方法,则点![]() 的坐标可表示为( )
的坐标可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=![]() (k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=
(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=![]() (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
(1)求反比例函数的表达式.
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD.BC上,且DE=BP=1.连接BE,EC,AP,DP,PD与CE交于点F,AP与BE交于点H.
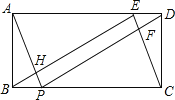
(1)判断△BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形,并证明你的判断;
(3)求四边形EFPH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③AM平分∠ADF;④AB+AC=2AE;其中正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日是我国第六个南京大屠杀难者国家公祭日,某校决定开展铭记历史珍爱和平”主题演讲比赛,其中八(1)班要从甲、乙两名参赛选手中择优推荐一人参加校级决赛,他们预赛阶段的各项得分如下表:
日是我国第六个南京大屠杀难者国家公祭日,某校决定开展铭记历史珍爱和平”主题演讲比赛,其中八(1)班要从甲、乙两名参赛选手中择优推荐一人参加校级决赛,他们预赛阶段的各项得分如下表:
项目 选手 | 演讲内容 | 演讲技巧 | 仪表形象 |
甲 |
|
|
|
乙 |
|
|
|
(1)如果根据三项成绩的平均分确定推荐人选,请通过计算说明甲、乙两人谁会被推荐
(2)如果根据演讲内容、演讲技、巧仪表形象按![]() 的比例确定成绩,请通过计算说明甲、乙两人谁会被推荐,并对另外一位同学提出合理的建议.
的比例确定成绩,请通过计算说明甲、乙两人谁会被推荐,并对另外一位同学提出合理的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com