
ЁОЬтФПЁПФГаЃзщжЏвЛЯюЧђРрЖдПЙШќЃЌдкБОаЃЫцЛњЕїВщСЫШєИЩУћбЇЩњЃЌЖдЫћУЧУПШЫзюЯВЛЖЕФЧђРрдЫЖЏНјааСЫЭГМЦЃЌВЂЛцжЦШчЭМ1ЁЂЭМ2ЫљЪОЕФЬѕаЮКЭЩШаЮЭГМЦЭМЃЎ
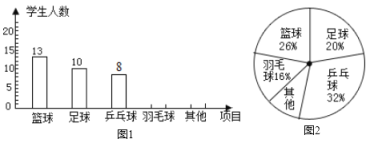
ИљОнЭГМЦЭМжаЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓБОДЮБЛЕїВщЕФбЇЩњШЫЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉШєШЋаЃга1500УћбЇЩњЃЌЧыФуЙРМЦИУаЃзюЯВЛЖРКЧђдЫЖЏЕФбЇЩњШЫЪ§ЃЛ
ЃЈ3ЃЉИљОнЕїВщНсЙћЃЌЧыФуЮЊбЇаЃМДНЋзщжЏЕФвЛЯюЧђРрБШШќЬсГіКЯРэЛЏНЈвщЃЎ
ЁОД№АИЁПЃЈ1ЃЉБОДЮЕїВщЕФШЫЪ§ЪЧ50ШЫЃЌВЙЭММћНтЮіЃЛЃЈ2ЃЉИУаЃзюЯВЛЖРКЧђдЫЖЏЕФбЇЩњдМ390ШЫЃЛЃЈ3ЃЉгЩгкЯВЛЖг№УЋЧђЕФШЫЪ§зюЖрЃЌбЇаЃгІзщжЏвЛГЁг№УЋЧђБШШќЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУРКЧђЕФШЫЪ§гыЫљеМЕФАйЗжБШМДПЩЧѓГізмЪ§ЃЛШЛКѓРћгУзмЪ§ЧѓГіг№УЋЧђКЭЦфЫћЕФШЫЪ§ЃЌМДПЩВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉгУ1500ГЫЯВЛЖРКЧђЕФШЫЫљеМЕФАйЗжБШ26%МДПЩЕУГіД№АИЃЛ
ЃЈ3ЃЉИљОнЯВЛЖг№УЋЧђЕФШЫЪ§зюЖрЃЌПЩвдНЈвщбЇаЃзщжЏг№УЋЧђБШШќЃЎ
ЃЈ1ЃЉ![]() ЃЌ
ЃЌ
![]() БОДЮЕїВщЕФШЫЪ§ЪЧ50ШЫЃЌ
БОДЮЕїВщЕФШЫЪ§ЪЧ50ШЫЃЌ
ЯВЛЖг№УЋЧђЕФШЫЪ§ЮЊЃК![]() ЃЈШЫЃЉ
ЃЈШЫЃЉ
ЯВЛЖЦфЫћЕФШЫЪ§ЮЊ![]() ЃЈШЫЃЉ
ЃЈШЫЃЉ
ЭГМЦЭМШчЭМЃК
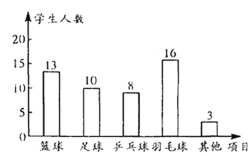
ЃЈ2ЃЉ![]() ЃЌ
ЃЌ
![]() ИУаЃзюЯВЛЖРКЧђдЫЖЏЕФбЇЩњдМ390ШЫЃЎ
ИУаЃзюЯВЛЖРКЧђдЫЖЏЕФбЇЩњдМ390ШЫЃЎ
ЃЈ3ЃЉгЩгкЯВЛЖг№УЋЧђЕФШЫЪ§зюЖрЃЌбЇаЃгІзщжЏвЛГЁг№УЋЧђБШШќЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
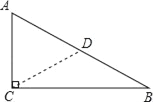
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAC=![]() ABЃЎЧѓжЄЃКЁЯB=30ЁуЃЎ
ABЃЎЧѓжЄЃКЁЯB=30ЁуЃЎ
ЧыЬюПеЭъГЩЯТСажЄУїЃЎ
жЄУїЃКШчЭМЃЌзїRtЁїABCЕФаББпЩЯЕФжаЯпCDЃЌ
дђ CD=![]() AB=AD ЃЈЁЁ ЁЁЃЉЃЎ
AB=AD ЃЈЁЁ ЁЁЃЉЃЎ
ЁпAC=![]() ABЃЌ
ABЃЌ
ЁрAC=CD=AD МДЁїACDЪЧЕШБпШ§НЧаЮЃЎ
ЁрЁЯA=ЁЁ ЁЁЁуЃЎ
ЁрЁЯB=90ЁуЉЁЯA=30ЁуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛЬѕЕРТЗЩЯЃЌМзГЕДг![]() ЕиЕН
ЕиЕН![]() ЕиЃЌввГЕДг
ЕиЃЌввГЕДг![]() ЕиЕН
ЕиЕН![]() ЕиЃЌввЯШГіЗЂЃЌЭМжаЕФелЯпЖЮБэЪОМзЁЂввСНГЕжЎМфЕФОрРы
ЕиЃЌввЯШГіЗЂЃЌЭМжаЕФелЯпЖЮБэЪОМзЁЂввСНГЕжЎМфЕФОрРы![]() ЃЈЧЇУзЃЉгыааЪЛЪБМф
ЃЈЧЇУзЃЉгыааЪЛЪБМф![]() ЃЈаЁЪБЃЉЕФКЏЪ§ЙиЯЕЕФЭМЯѓЃЌИљОнЭМЯѓНтОівдЯТЮЪЬтЃК
ЃЈаЁЪБЃЉЕФКЏЪ§ЙиЯЕЕФЭМЯѓЃЌИљОнЭМЯѓНтОівдЯТЮЪЬтЃК
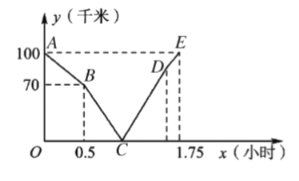
ЃЈ1ЃЉввЯШГіЗЂЕФЪБМфЮЊ аЁЪБЃЌввГЕЕФЫйЖШЮЊ ЧЇУз/ЪБЃЛ
ЃЈ2ЃЉЧѓЯпЖЮ![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСП
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉМзЁЂввСНГЕЫЯШЕНжеЕуЃЌЯШЕНЖрЩйЪБМфЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§y=Љx+1гыХзЮяЯпy=![]() x2+bx+cНЛгкAЃЈ0ЃЌ1ЃЉЃЌBСНЕуЃЌBЕузнзјБъЮЊ10ЃЌХзЮяЯпЕФЖЅЕуЮЊCЃЎ
x2+bx+cНЛгкAЃЈ0ЃЌ1ЃЉЃЌBСНЕуЃЌBЕузнзјБъЮЊ10ЃЌХзЮяЯпЕФЖЅЕуЮЊCЃЎ
ЃЈ1ЃЉЧѓbЃЌcЕФжЕЃЛ
ЃЈ2ЃЉХаЖЯЁїABCЕФаЮзДВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕуDЁЂEЗжБ№ЮЊЯпЖЮABЁЂBCЩЯШЮвтвЛЕуЃЌСЌНгCDЃЌШЁCDЕФжаЕуFЃЌСЌНгAFЃЌEFЃЎЕБЫФБпаЮADEFЮЊЦНааЫФБпаЮЪБЃЌЧѓЦНааЫФБпаЮADEFЕФжмГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжЊЪЖБГОА
ЮвУЧдкЕкЪЎвЛеТЁЖШ§НЧаЮЁЗжабЇЯАСЫШ§НЧаЮЕФБпгыНЧЕФаджЪЃЌдкЕкЪЎЖўеТЁЖШЋЕШШ§НЧаЮЁЗжабЇЯАСЫШЋЕШШ§НЧаЮЕФаджЪКЭХаЖЈЃЌдкЪЎШ§еТЁЖжсЖдГЦЁЗжабЇЯАСЫЕШбќШ§НЧаЮЕФаджЪКЭХаЖЈЃЎдквЛаЉЬНОПЬтжаОГЃгУвдЩЯжЊЪЖзЊЛЏНЧКЭБпЃЌНјЖјНтОіЮЪЬт

ЮЪЬтГѕЬН
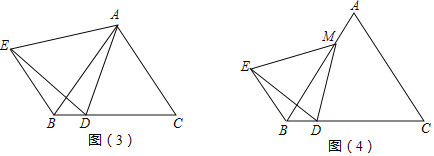
ШчЭМЃЈ1ЃЉЃЌЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃЌЕуDЪЧBCЩЯвЛЕуЃЌСЌНгADЃЌвдADЮЊвЛБпзїЁїADEЃЌЪЙЁЯDAEЃН90ЁуЃЌADЃНAEЃЌСЌНгBEЃЌВТЯыBEКЭCDгадѕбљЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
РрБШдйЬН
ШчЭМЃЈ2ЃЉЃЌЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃЌЕуMЪЧABЩЯвЛЕуЃЌЕуDЪЧBCЩЯвЛЕуЃЌСЌНгMDЃЌвдMDЮЊвЛБпзїЁїMDEЃЌЪЙЁЯDMEЃН90ЁуЃЌMDЃНMEЃЌСЌНгBEЃЌдђЁЯEBDЃНЁЁ ЁЁЃЎЃЈжБНгаДГіД№АИЃЌВЛаДЙ§ГЬЃЌЕЋвЊЧѓзїГіИЈжњЯпЃЉ
ЗНЗЈЧЈвЦ
ШчЭМЃЈ3ЃЉЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЕуDЪЧBCЩЯвЛЕуЃЌСЌНгADЃЌвдADЮЊвЛБпзїЕШБпШ§НЧаЮADEЃЌСЌНгBEЃЌдђBDЁЂBEЁЂBCжЎМфгадѕбљЕФЪ§СПЙиЯЕЃПЁЁ ЁЁЃЈжБНгаДГіД№АИЃЌВЛаДЙ§ГЬЃЉЃЎ
ЭиеЙДДаТ
ШчЭМЃЈ4ЃЉЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЕуMЪЧABЩЯвЛЕуЃЌЕуDЪЧBCЩЯвЛЕуЃЌСЌНгMDЃЌвдMDЮЊвЛБпзїЕШБпШ§НЧаЮMDEЃЌСЌНгBEЃЎВТЯыЁЯEBDЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉзїЭМЗЂЯжЃК
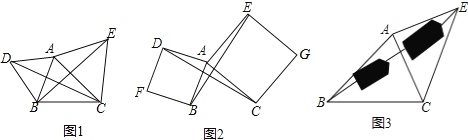
ШчЭМ1ЃЌвбжЊ![]() ЃЌаЁКЭЌбЇвд
ЃЌаЁКЭЌбЇвд![]() ЁЂ
ЁЂ![]() ЮЊБпЯђ
ЮЊБпЯђ![]() ЭтзїЕШБп
ЭтзїЕШБп![]() КЭЕШБп
КЭЕШБп![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎетЪБЫћЗЂЯж
ЃЎетЪБЫћЗЂЯж![]() гы
гы![]() ЕФЪ§СПЙиЯЕЪЧ ЃЎ
ЕФЪ§СПЙиЯЕЪЧ ЃЎ
ЃЈ2ЃЉЭиеЙЬНОПЃК
ШчЭМ2ЃЌвбжЊ![]() ЃЌаЁКЭЌбЇвд
ЃЌаЁКЭЌбЇвд![]() ЁЂ
ЁЂ![]() ЮЊБпЯђЭтзїе§ЗНаЮ
ЮЊБпЯђЭтзїе§ЗНаЮ![]() КЭе§ЗНаЮ
КЭе§ЗНаЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌЪдХаЖЯ
ЃЌЪдХаЖЯ![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉНтОіЮЪЬт
ШчЭМ3ЃЌвЊВтСПГиЬССНАЖЯрЖдЕФСНЕу![]() ЃЌ
ЃЌ![]() ЕФОрРыЃЌвбОВтЕУ
ЕФОрРыЃЌвбОВтЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() УзЃЌ
УзЃЌ![]() ЃЌдђ
ЃЌдђ![]() УзЃЎ
УзЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
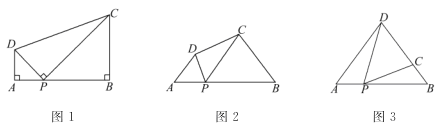
ЁОЬтФПЁП(1)ЁЂЮЪЬтЃКШчЭМ1ЃЌдкЫФБпаЮABCDжаЃЌЕуPЮЊABЩЯвЛЕуЃЌЁЯDPC=ЁЯA=ЁЯB=90ЁуЃЎЧѓжЄЃКADЁЄBC=APЁЄBPЃЎ
(2)ЁЂЬНОПЃКШчЭМ2ЃЌдкЫФБпаЮABCDжаЃЌЕуPЮЊABЩЯвЛЕуЃЌЕБЁЯDPC=ЁЯA=ЁЯB=ІШЪБЃЌЩЯЪіНсТлЪЧЗёвРШЛГЩСЂЃПЫЕУїРэгЩЃЎ
(3)ЁЂгІгУЃКЧыРћгУЃЈ1ЃЉЃЈ2ЃЉЛёЕУЕФОбщНтОіЮЪЬтЃК
ШчЭМ3ЃЌдкЁїABDжаЃЌAB=6ЃЌAD=BD=5ЃЎЕуPвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЃЌгЩЕуA ГіЗЂЃЌбиБпABЯђЕуBдЫЖЏЃЌЧвТњзуЁЯDPC=ЁЯAЃЎЩшЕуPЕФдЫЖЏЪБМфЮЊtЃЈУыЃЉЃЌЕБDCЕФГЄгыЁїABDЕзБпЩЯЕФИпЯрЕШЪБЃЌЧѓtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
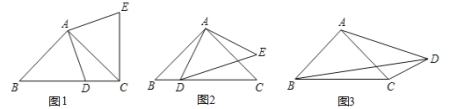
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌDЪЧBCЕФжаЕуЃЌЙ§DЕуЕФжБЯпGFНЛACгкFЃЌНЛACЕФЦНааЯпBGгкGЕуЃЌDEЁЭDFЃЌНЛABгкЕуEЃЌСЌНсEGЁЂEFЃЎ
ЃЈ1ЃЉЧѓжЄЃКBGЃНCFЃЛ
ЃЈ2ЃЉЧыФуХаЖЯBE+CFгыEFЕФДѓаЁЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЃКШчЭМ![]() дк
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() БпЩЯвЛЕуЃЈВЛгыЕу
БпЩЯвЛЕуЃЈВЛгыЕу![]() ЃЌ
ЃЌ![]() жиКЯЃЉЃЌСЌНг
жиКЯЃЉЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌВЂТњзу
ЃЌВЂТњзу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎдђЯпЖЮ
ЃЎдђЯпЖЮ![]() КЭЯпЖЮ
КЭЯпЖЮ![]() ЕФЪ§СПЙиЯЕЪЧ_______ЃЌЮЛжУЙиЯЕЪЧ_______ЃЎ
ЕФЪ§СПЙиЯЕЪЧ_______ЃЌЮЛжУЙиЯЕЪЧ_______ЃЎ
ЃЈ2ЃЉЬНЫїЃКШчЭМ![]() ЃЌЕБ
ЃЌЕБ![]() ЕуЮЊ
ЕуЮЊ![]() БпЩЯвЛЕуЃЈВЛгыЕу
БпЩЯвЛЕуЃЈВЛгыЕу![]() ЃЌ
ЃЌ![]() жиКЯЃЉЃЌ
жиКЯЃЉЃЌ![]() гы
гы![]() ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЪдЬНЫїЯпЖЮ
ЃЎЪдЬНЫїЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфТњзуЕФЕШСПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
жЎМфТњзуЕФЕШСПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ3ЃЉЭиеЙЃКШчЭМ![]() ЃЌдкЫФБпаЮ
ЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧыжБНгаДГіЯпЖЮ
ЃЌЧыжБНгаДГіЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com