
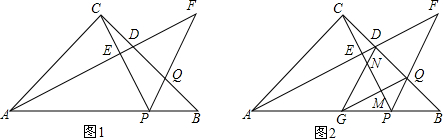
分析 (1)首先根据∠ACB=90°,AC=BC,可得∠BAC=∠ABC=45°;然后根据三角形的外角的性质,可得∠FDQ=∠FAB+∠ABC=∠FAB+45°;最后在△BPQ中,根据三角形的内角和定理,推得∠FQD=∠BQP=∠FAB+45°,即可推得∠FDQ=∠FQD.
(2)MN与EN的数量关系是:MN=3EN.首先判断出AH∥DG∥PQ,推得$\frac{BP}{PA}=\frac{BQ}{QH}$,再根据相似三角形判定的方法,判断出△APC∽△BPQ,推得$\frac{BP}{PA}=\frac{BQ}{AC}=\frac{BQ}{BC}$,进一步推得BQ=HC=CD;然后判断出AH∥PF,推得$\frac{DQ}{DH}=\frac{FD}{AD}=\frac{GQ}{AD}$=$\frac{BQ}{BD}$,进一步推得DQ=CD,BP=PG,再根据BI∥GQ,推得BI=GM;最后判断出AD∥BI,即可推得$\frac{DE}{BI}=\frac{CD}{BC}=\frac{1}{3}$,据此判断出MN=3EN即可.
解答 (1)证明:如图1,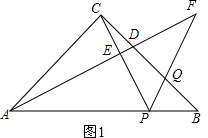 ,
,
∵∠ACB=90°,AC=BC,
∴∠BAC=∠ABC=45°,
由三角形的外角的性质,可得
∠FDQ=∠FAB+∠ABC=∠FAB+45°,
∵AD⊥PC,
∴∠AEP=90°,
∴∠FAB+∠APC=90°,
∴∠APC=90°-∠FAB,
又∵∠BPQ=∠APC,
∴∠BPQ=90°-∠FAB,
∴∠FQD=∠BQP=180°-∠BPQ-∠ABC
=180°-(90°-∠FAB)-45°
=∠FAB+45°
∴∠FDQ=∠FQD.
(2)解:MN与EN的数量关系是:MN=3EN.
如图2,延长DC至H,使HC=CD,连接AH,过点B作BI∥GQ,交CP延长线于点I,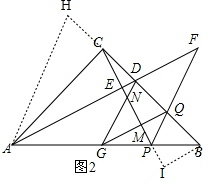 ,
,
∵HC=CD,AC⊥HD,
∴△ADH是等腰三角形,
∴AD=AH,
∴∠H=∠ADH=∠FDQ=∠FQD=∠BQP,
∵把△DFQ沿DQ边翻折,得到△DGQ,
∴△GDQ≌△FDQ,
∴∠FDQ=∠GDQ,
又∵∠H=∠FDQ=∠BQP,
∴∠H=∠BQP=∠GDQ,
∴AH∥DG∥PQ,
∴$\frac{BP}{PA}=\frac{BQ}{QH}$,∠GQP=∠DGQ,
在△APC和△BPQ中,
$\left\{\begin{array}{l}{∠APC=∠BPQ}\\{∠CAP=∠QBP=45°}\end{array}\right.$
∴△APC∽△BPQ,
∴$\frac{BP}{PA}=\frac{BQ}{AC}=\frac{BQ}{BC}$,
又∵$\frac{BP}{PA}=\frac{BQ}{QH}$,
∴$\frac{BQ}{BC}=\frac{BQ}{QH}$,
∴BC=QH,
∴BQ=HC,
又∵HC=CD,
∴BQ=HC=CD.
∵把△DFQ沿DQ边翻折,得到△DGQ,
∴∠DFQ=∠DGQ,
又∵∠GQP=∠DGQ,
∴∠GQP=∠DFQ,
∴AD∥GQ,四边形DFQG是平行四边形,
∴$\frac{MN}{EN}=\frac{GM}{DE}$,FD=GQ,
∵AH∥PF,
∴$\frac{DQ}{DH}=\frac{FD}{AD}=\frac{GQ}{AD}$=$\frac{BQ}{BD}$,
又∵DH=2CD,BQ=CD,
∴$\frac{DQ}{2CD}=\frac{CD}{BD}$,
∴$\frac{DQ}{2CD}=\frac{CD}{CD+DQ}$,
∴(DQ+2CD)(DQ-CD)=0,
解得DQ=CD,或DQ=-2CD(舍去),
∵$\frac{BP}{PG}=\frac{BQ}{DQ}$=1,
∴BP=PG,
∵BI∥GQ,
∴$\frac{BI}{GM}=\frac{BP}{PG}$=1,
∴BI=GM,
∵BI∥GQ,AD∥GQ,
∴AD∥BI,
∴$\frac{DE}{BI}=\frac{CD}{BC}=\frac{1}{3}$,
∴$\frac{DE}{GM}=\frac{1}{3}$,
∴$\frac{MN}{EN}=\frac{GM}{DE}=3$,
∴MN=3EN.
点评 (1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了数形结合思想的应用,考查了空间想象能力,要熟练掌握.
(2)此题还考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.
(3)此题还考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.


科目:初中数学 来源: 题型:填空题
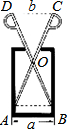 如图,质地均匀的空心圆柱形零件的外直径为a,现用一个交叉钳(AC和BD的长相等)测量,如果$\frac{OA}{OC}=\frac{OB}{OD}=n$,而且CD=b,那么这个零件的厚度为$\frac{a-bn}{2}$.
如图,质地均匀的空心圆柱形零件的外直径为a,现用一个交叉钳(AC和BD的长相等)测量,如果$\frac{OA}{OC}=\frac{OB}{OD}=n$,而且CD=b,那么这个零件的厚度为$\frac{a-bn}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
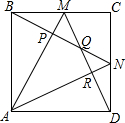 如图,M、N是单位正方形ABCD边BC、CD的中点,连接AM、DM、AN、BN,则这些线段所围成的四边形APQR的面积是$\frac{4}{15}$.
如图,M、N是单位正方形ABCD边BC、CD的中点,连接AM、DM、AN、BN,则这些线段所围成的四边形APQR的面积是$\frac{4}{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{50x+40(12-x)≥520}\\{15x+25(12-x)≥240}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{50x+40(12-x)>520}\\{15x+25(12-x)>240}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{50x+40(12-x)≤520}\\{15x+25(12-x)≤240}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{50x+40(12-x)<520}\\{15x+25(12-x)<240}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com