
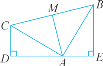
【题目】如图,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.
(1)求证:AC=BA.
(2)△ABC是什么三角形?请说明理由.
(3)如果AM⊥BC,那么AM=![]() BC吗?请说明理由.
BC吗?请说明理由.
【答案】(1)见解析;(2)△ABC是等腰直角三角形.理由见解析;(3)AM=![]() BC.理由见解析.
BC.理由见解析.
【解析】(1)AC=AB,可通过证明△ADC≌△AEB得到;
(2)△ABC是等腰直角三角形,由(1)可知△ABC是等腰三角形,再证明∠CAB=90°即可;
(3)AM=![]() BC,根据等腰三角形的性质:三线合一证明即可.
BC,根据等腰三角形的性质:三线合一证明即可.
(1)在△ACD和△BAE中,
∵CD=AE,∠CDA=∠AEB=90°,AD=BE,
∴△ACD≌△BAE(SAS).∴AC=BA.
(2)△ABC是等腰直角三角形.理由如下:
由(1)知△ACD≌△BAE,
∴AC=BA,∠CAD=∠ABE,
∴∠BAC=180°-∠CAD-∠BAE=180°-∠ABE-∠BAE=180°-90°=90°.
∴△ABC为等腰直角三角形.
(3)AM=![]() BC.理由如下:
BC.理由如下:
∵△ABC为等腰直角三角形,且AM⊥BC,
∴BM=CM,∴AM=![]() BC.
BC.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,……以此类推,则a2018的值为( )
A. ﹣1007 B. ﹣1008 C. ﹣1009 D. ﹣2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是( )
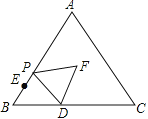
A. 8 B. 10 C. 3π D. 5π
查看答案和解析>>
科目:初中数学 来源: 题型:
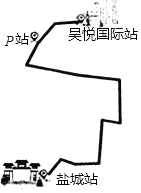
【题目】常州每年举行一次“一袋牛奶的暴走”公益活动,用步行的方式募集善款,其中挑战型路线”的起点是淹城站,并沿着规定的线路到达终点吾悦国际站.甲、乙两组市民从起点同时出发,已知甲组的速度为6km/h,乙组的速度为5km/h,当甲组到达终点后,立即以3km/h的速度按原线路返回,并在途中的P站与乙组相遇,P站与吾悦国际站之间的路程为1.5km
(1)求“挑战型路线”的总长;
(2)当甲组到达终点时,乙组离终点还有多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A=90°,AB=AC , BC=63cm,现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是从下往上数第张.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P为AB上一点,则下列四个条件中, ①∠ACP=∠B②∠APC=∠ACB③ ![]() ④ABCP=APCB ,
④ABCP=APCB ,
其中能满足△APC和△ACB相似的条件有( )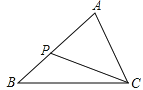
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com