【题目】如图，△ABC中，∠C＝90°，∠A＝60°.
（1）尺规作图：作△ABC的角平分线AD（不写作法，保留作图痕迹）；
（2）画DE⊥AB，垂足为E；
（3）若BC＝12cm，求DE的长.
寒假天地重庆出版社系列答案科目：初中数学 来源： 题型：
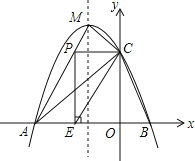
【题目】如图，抛物线
与x轴交于A、B两点，与y轴交于点
，且此抛物线的顶点坐标为
．
求此抛物线的解析式；
设点D为已知抛物线对称轴上的任意一点，当
与
面积相等时，求点D的坐标；
点P在线段AM上，当PC与y轴垂直时，过点P作x轴的垂线，垂足为E，将
沿直线CE翻折，使点P的对应点
与P、E、C处在同一平面内，请求出点坐标，并判断点是否在该抛物线上．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图①，若AB∥CD，求∠B+∠D+∠E1的度数？
（2）如图②，若AB∥CD，求∠B+∠D+∠E1+∠E2的度数？
（3）如图③，若AB∥CD，求∠B+∠D+∠E1+∠E2+∠E3的度数？
（4）如图④，若AB∥CD，猜想∠B+∠D+∠E1+∠E2+…+∠En的度数？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一个三角形的两条边长为1cm和2cm，一个内角为45°．
（1）请你利用如图45°角，画出一个满足题设条件的三角形．
（2）你是否还能画出既满足题设条件，又与（1）中所画的不全等的三角形？若能，请用“尺规作图”画出，若不能，请说明理由．
（3）如果将题设条件改为“一个三角形的两条边长为3cm和4cm，一个内角为45°”，画出满足这一条件的，且彼此不全等的所有三角形．（要求在图中标记3cm和4cm的边长）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（问题原型）如图1，在四边形ABCD中，
，
点E、F分别为AC、BC的中点，连结EF，
试说明：
．
（探究）如图2，在问题原型的条件下，当AC平分
，
时，求的大小．
（应用）如图3，在问题原型的条件下，当
，且四边形CDEF是菱形时，直接写出四边形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是-块长方形空地，长为
米，宽为
米，现要对其进行修整，在空白部分铺设
条宽度为
米的小路，其余阴影部分种植草坪．
（1）用整式表示小路的面积；
（2）用整式表示草坪的面积；
（3）现有两种修整方案，方案一：修建小路的宽度为
米；方案二：修建小路的宽度为米．铺设小路的造价为每平方米
元，种植草坪的造价为每平方米
元，请问选用哪种方案最划算．( 写出计算过程)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
平分
.
（1）若
为线段上的一个点，过点作
交线段
的延长线于点
①若
，
，则
；
②猜想
与
、
之间的数量关系，并给出证明．
（2）若在线段的延长线上，过点作交直线于点．请你做出示意图，直接写出
与
、的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，已知∠A＝α．
（1）如图1，∠ABC、∠ACB的平分线相交于点D．
①当α＝70°时，∠BDC度数＝ 度（直接写出结果）；
②∠BDC的度数为 （用含α的代数式表示）；
（2）如图2，若∠ABC的平分线与∠ACE角平分线交于点F，求∠BFC的度数（用含α的代数式表示）．
（3）在（2）的条件下，将△FBC以直线BC为对称轴翻折得到△GBC，∠GBC的角平分线与∠GCB的角平分线交于点M（如图3），求∠BMC的度数（用含α的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
，其顶点坐标为
，抛物线与x轴的一个交点为
，直线
与抛物线交于A，B两点，下列结论：
，
，
方程
有两个相等的实数根，
抛物线与x轴的另一个交点是
，
当
时，有
其中正确结论的个数是
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
