
【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7)、(-3,0)、(0,3).

(1)画出△ABC,并求△ABC的面积.
(2)在平面直角坐标系中平移△ABC,使点C经过平移后的对应点为C'(5,4),平移后△ABC得到△A'B'C',画出平移后的△A'B'C',并写出点A',B'的坐标
(3)P(-3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,-3),则m= n=
【答案】(1)见解析;(2)见解析,A′(﹣1,8),B′(2,1);(3)﹣9,1.
【解析】
(1)根据各点在坐标系中的位置描出各点,并顺次连接即可,面积利用矩形面积减去三角形面积求解;
(2)根据图形平移的性质画出平移后的△A′B′C′,并写出点A′,B′的坐标即可;
(3)根据点平移的性质即可得出m、n的值.
解:
(1)如图,△ABC即为所求
 ;
;
作辅助线,过AF⊥x轴,垂足是F, AE⊥y轴,垂足是E.
△ABC的面积=S矩形AFOE-S△AFE- S△BCO- S△AEC
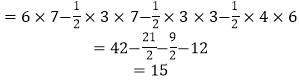
即面积是15.
(2)C(0,3)经过平移后的对应点为C′(5,4),则C点即为,向上平移1个单位,向右平移5个单位,相应的A,B,也一样平移即可得到:如图,△A′B′C′即为所求,A′(﹣1,8),B′(2,1);
(3)∵P(﹣3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,﹣3),
∴n=﹣3+4=1,m+6=﹣3,
∴n=1,m=﹣9.
故答案为:﹣9,1.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个钝角△ABC(其中∠ABC=120°)绕
点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连结AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.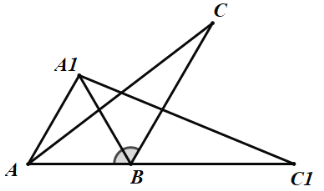
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,4),且满足(a+4)2+![]() =0,过C作CB⊥x轴于B。
=0,过C作CB⊥x轴于B。

(1)求三角形ABC的面积;
(2)如图2,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列长度的四组线段:①1,![]() ,
,![]() ;②3,4,5;③6,7,8;④a2-1,a2+1,2a(a为大于1的正整数).其中能组成直角三角形的有( )
;②3,4,5;③6,7,8;④a2-1,a2+1,2a(a为大于1的正整数).其中能组成直角三角形的有( )
A.①②③B.①②④C.①②D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD= ![]() ,以对角线BD为直径的⊙O与CD切于点D,与BC交于点E,∠ABD=30°,则图中阴影部分的面积为 . (不取近似值)
,以对角线BD为直径的⊙O与CD切于点D,与BC交于点E,∠ABD=30°,则图中阴影部分的面积为 . (不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①在同一平面内不相交的两条线段必平行
②过两条直线![]() 外一点
外一点![]() ,一定可做直线
,一定可做直线![]() ,使
,使![]() ,且
,且![]()
③过直线外一点有且只有一条直线与已知直线平行
④两直线被第三条直线所截得的同旁内角的平分线互相垂直
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com