
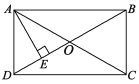
【题目】如图,在矩形ABCD中,对角线AC与BD交于点O,且△ADO为等边三角形,过点A作AE⊥BD于点E.
(1)求∠ABD的度数;
(2)若BD=10,求AE的长.
【答案】(1)∠ABD=30°;(2)AE=![]() .
.
【解析】
(1)根据矩形性质得出∠DAB=90°,求出∠ADB=60°,代入∠ABD=180°-∠DAB-∠ADB求出即可;
(2)求出AD,根据等腰三角形性质得出DE=EO,求出DE,根据勾股定理求出即可.
(1)∵四边形ABCD是矩形,∴∠DAB=90°,
∵△ADO为等边三角形,∴∠ADB=60°,
∴∠ABD=180°-∠DAB-∠ADB=30°;
(2)∵BD=10,∠BAD=90°,∠ABD=30°,
∴AD=![]() BD=5,
BD=5,
∵△ADO为等边三角形,∴AD=AO=DO=5,
∵AE⊥DO,∴DE=EO=![]() DO=2.5,
DO=2.5,
在Rt△AED中,由勾股定理得AE=![]() .
.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
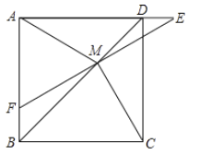
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 、
、![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]()
![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一次函数![]() 的图象分别交x轴、y轴于点A,B,与反比例函数
的图象分别交x轴、y轴于点A,B,与反比例函数![]() 图象在第二象限交于点C(m,6),
图象在第二象限交于点C(m,6),![]() 轴于点D,OA=OD.
轴于点D,OA=OD.
(1)求m的值和一次函数的表达式;
(2)在X轴上求点P,使△CAP为等腰三角形(求出所有符合条件的点)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的![]() ,则梯子比较稳定,如图,AB为一长度为6米的梯子.
,则梯子比较稳定,如图,AB为一长度为6米的梯子.
(1)当梯子稳定摆放时,它的顶端能达到5.7米高的墙头吗?
(2)如图2,若梯子底端向左滑动(3![]() ﹣2)米,那么梯子顶端将下滑多少米?
﹣2)米,那么梯子顶端将下滑多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2![]() ,
,![]() .△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子总结惨痛教训后.决定和乌龟再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(![]() 表示乌龟从起点出发所行的时间,
表示乌龟从起点出发所行的时间,![]() 表示乌龟所行的路程,
表示乌龟所行的路程,![]() 表示兔子所行的路程.下列说法中:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处上了乌龟.正确的有:( )
表示兔子所行的路程.下列说法中:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处上了乌龟.正确的有:( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 种商品以每件30元出售,
种商品以每件30元出售,![]() 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共1000件,且
两种商品共1000件,且![]() 种商品的数量不少于
种商品的数量不少于![]() 种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com