
【题目】生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的![]() ,则梯子比较稳定,如图,AB为一长度为6米的梯子.
,则梯子比较稳定,如图,AB为一长度为6米的梯子.
(1)当梯子稳定摆放时,它的顶端能达到5.7米高的墙头吗?
(2)如图2,若梯子底端向左滑动(3![]() ﹣2)米,那么梯子顶端将下滑多少米?
﹣2)米,那么梯子顶端将下滑多少米?

【答案】(1)它的顶端不能到达5.7米高的墙头;(2)梯子的顶端将下滑动![]() 米.
米.
【解析】
(1)由题意可得,AB=6m,OB=![]() AB=2m,在Rt△AOB中,由勾股定理求得OA的长,与5.7比较即可得结论;(2)由题意求得OD= 3
AB=2m,在Rt△AOB中,由勾股定理求得OA的长,与5.7比较即可得结论;(2)由题意求得OD= 3![]() 米, 在Rt△DOC中,由勾股定理求得OC的长,即可求得AC的长,由此即可求得结论.
米, 在Rt△DOC中,由勾股定理求得OC的长,即可求得AC的长,由此即可求得结论.
(1)由题意可得,AB=6m,OB=![]() AB=2m,
AB=2m,
在Rt△AOB中,由勾股定理可得,
AO=![]() m,
m,
∵4![]() <5.7,
<5.7,
∴梯子的顶端不能到达5.7米高的墙头;
(2)因梯子底端向左滑动(3![]() ﹣2)米,
﹣2)米,
∴BD=(3![]() ﹣2)米,
﹣2)米,
∴OD=OB+BD=3![]() 米,
米,
在Rt△DOC中,由勾股定理可得,
OC=![]() 米,
米,
∴AC=OA-OC=![]() -
-![]() =
=![]() 米.
米.
∴梯子的顶端将下滑动![]() 米.
米.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°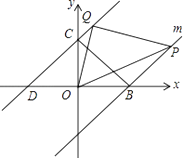
(1)则∠PBO=度;
(2)问:PBCQ的值是否为定值?如果是,请求出该定值;如果不是,请说明理由;
(3)求证:CQ2+PB2=PQ2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC和BD相交于点O,过O作EF⊥AC,交AD于E,交BC于F,连接AF、CE. 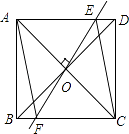
(1)求证:四边形AECF是菱形
(2)若AB=3,BC=4,则菱形AECF的周长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):

(1)当a=2时,某用户一个月用了28 m3水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为n 立方米,当n>20时,则该用户应缴纳的水费________元(用含a、n的整式表示);
(3)当a=2时,甲、乙两用户一个月共用水40m3 ,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3 ,试求甲、乙两用户一个月共缴纳的水费(用含x的整式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王乘公共汽车从甲地到相距40千米的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车多20千米/时,回来时路上所花时间比去时节省了 ![]() ,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
A.![]() =
= ![]() ×
× ![]()
B.![]() =
= ![]() ×
× ![]()
C.![]() +
+ ![]() =
= ![]()
D.![]() ﹣
﹣ ![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4厘米,动点P从点A出发沿AB边由A向B以1厘米/秒的速度匀速移动(点P不与点A、B重合),动点Q从点B出发沿拆线BC-CD以2厘米/秒的速度匀速移动。点P、Q同时出发,当点P停止运动,点Q也随之停止。联结AQ交BD于点E。设点P运动时间为t秒。
(1)用t表示线段PB的长;
(2)当点Q在线段BC上运动时,t为何值时,∠BEP和∠BEQ相等;
(3)当t为何值时,线段P、Q之间的距离为2![]() cm.
cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,将小旗ACDB放于平面直角坐标系中,得到各顶点的坐标为A(﹣6,12),B(﹣6,0),C(0,6),D(﹣6,6).以点B为旋转中心,在平面直角坐标系内将小旗顺时针旋转90°. 
(1)画出旋转后的小旗A′C′D′B′;
(2)写出点A′,C′,D′的坐标;
(3)求出线段BA旋转到B′A′时所扫过的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的顶点为(0,4)且与x轴交于(﹣2,0),(2,0).
(1)直接写出抛物线解析式;
(2)如图,将抛物线向右平移k个单位,设平移后抛物线的顶点为D,与x轴的交点为A、B,与原抛物线的交点为P.
①当直线OD与以AB为直径的圆相切于E时,求此时k的值;
②是否存在这样的k值,使得点O、P、D三点恰好在同一条直线上?若存在,求出k值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com