
【题目】已知抛物线的顶点为(0,4)且与x轴交于(﹣2,0),(2,0).
(1)直接写出抛物线解析式;
(2)如图,将抛物线向右平移k个单位,设平移后抛物线的顶点为D,与x轴的交点为A、B,与原抛物线的交点为P.
①当直线OD与以AB为直径的圆相切于E时,求此时k的值;
②是否存在这样的k值,使得点O、P、D三点恰好在同一条直线上?若存在,求出k值;若不存在,请说明理由.
【答案】
(1)
解:∵抛物线的顶点为(0,4),
∴可设抛物线解析式为y=ax2+4,
又∵抛物线过点(2,0),
∴0=4a+4,解得a=﹣1,
∴抛物线解析式为y=﹣x2+4;
(2)
解:①如图,连接CE,CD.
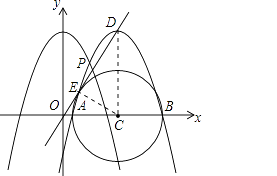
∵OD是⊙C的切线,∴CE⊥OD.
在Rt△CDE中,∠CED=90°,CE=AC=2,DC=4,
∴∠EDC=30°,
∴在Rt△CDO中,∠OCD=90°,CD=4,∠ODC=30°,
∴OC= ![]() ,
,
∴当直线OD与以AB为直径的圆相切时,k=OC= ![]() ;
;
②存在k=2 ![]() ,能够使得点O、P、D三点恰好在同一条直线上.理由如下:
,能够使得点O、P、D三点恰好在同一条直线上.理由如下:
设抛物线y=﹣x2+4向右平移k个单位后的解析式是y=﹣(x﹣k)2+4,它与y=﹣x2+4交于点P,
由﹣(x﹣k)2+4=﹣x2+4,解得x1= ![]() ,x2=0(不合题意舍去),
,x2=0(不合题意舍去),
当x= ![]() 时,y=﹣
时,y=﹣ ![]() k2+4,
k2+4,
∴点P的坐标是( ![]() ,﹣
,﹣ ![]() k2+4).
k2+4).
设直线OD的解析式为y=mx,把D(k,4)代入,
得mk=4,解得m= ![]() ,
,
∴直线OD的解析式为y= ![]() x,
x,
若点P( ![]() ,﹣
,﹣ ![]() k2+4)在直线y=
k2+4)在直线y= ![]() x上,得﹣
x上,得﹣ ![]() k2+4=
k2+4= ![]()
![]() ,
,
解得k=±2 ![]() (负值舍去),
(负值舍去),
∴当k=2 ![]() 时,O、P、D三点在同一条直线上.
时,O、P、D三点在同一条直线上.
【解析】(1)由抛物线的顶点为(0,4),可设抛物线解析式为y=ax2+4,再将点(2,0)代入,求出a=﹣1,即可得到抛物线解析式为y=﹣x2+4;(2)①连接CE,CD,先根据切线的性质得出CE⊥OD,再解Rt△CDE,得出∠EDC=30°,然后解Rt△CDO,得出OC= ![]() ,则k=OC=
,则k=OC= ![]() ;②设抛物线y=﹣x2+4向右平移k个单位后的解析式是y=﹣(x﹣k)2+4,它与y=﹣x2+4交于点P,先求出交点P的坐标是(
;②设抛物线y=﹣x2+4向右平移k个单位后的解析式是y=﹣(x﹣k)2+4,它与y=﹣x2+4交于点P,先求出交点P的坐标是( ![]() ,﹣
,﹣ ![]() k2+4),再利用待定系数法求出直线OD的解析式为y=
k2+4),再利用待定系数法求出直线OD的解析式为y= ![]() x,然后将点P的坐标代入y=
x,然后将点P的坐标代入y= ![]() x,即可求出k的值.
x,即可求出k的值.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


科目:初中数学 来源: 题型:
【题目】生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的![]() ,则梯子比较稳定,如图,AB为一长度为6米的梯子.
,则梯子比较稳定,如图,AB为一长度为6米的梯子.
(1)当梯子稳定摆放时,它的顶端能达到5.7米高的墙头吗?
(2)如图2,若梯子底端向左滑动(3![]() ﹣2)米,那么梯子顶端将下滑多少米?
﹣2)米,那么梯子顶端将下滑多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△AOB中,∠AOB=90°,AO=6厘米,BO=8厘米,分别以OB和OA所在直线为x轴,y轴建立平面直角坐标系,如图所示,动点M从点A开始沿AO方向以2厘米/秒的速度向点O移动,同时动点N从点O开始沿OB方向以4厘米/秒的速度向点B移动(其中一点到达终点时,另一点随即停止移动).
(1)求过点A和点B的直线表达式;
(2)当点M移动多长时间时,四边形AMNB的面积最小?并求出四边形AMNB面积的最小值;
(3)在点M和点N移动的过程中,是否存在以O,M,N为顶点的三角形与△AOB相似?若存在,请求出点M 和点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑶寨中学食堂为学生提供了四种价格的午餐供其选择,这四种价格分别是:A.3元,B.4元,C.5元,D.6元.为了了解学生对四种午餐的购买情况,学校随机抽样调查了甲、乙两班学生某天购买四种午餐的情况,依据统计数据制成如下的统计图表:
甲、乙两班学生购买午餐的情况统计表
品种 | A | B | C | D |
甲 | 6 | 22 | 16 | 6 |
乙 | ? | 13 | 25 | 3 |

(1)求乙班学生人数;
(2)求乙班购买午餐费用的中位数;
(3)已知甲、乙两班购买午餐费用的平均数为4.44元,从平均数和众数的角度解答,哪个班购买的午餐价格较高?
(4)从这次接受调查的学生中,随机抽查一人,恰好是购买C种午餐的学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.求证:
(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化建设中,某学校原计划按每班5幅订购了“名人字画”共90幅.由于新学期班数增加,决定从阅览室中取若干幅“名人字画”一起分发,如果每班分4幅,则剩下17幅;如果每班分5幅,则最后一班不足3幅,但不少于1幅.
(1)该校原有的班数是多少个?
(2)新学期所增加的班数是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家距离与时间之间的关系是(只需填序号). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com