Question

【题目】如图，在矩形ABCD中，E，F为BC上两点，且BE=CF，连接AF，DE交于点O．求证：

（1）△ABF≌△DCE；
（2）△AOD是等腰三角形．

Answer 1

【答案】
（1）

证明：在矩形ABCD中，∠B=∠C=90°，AB=DC，

∵BE=CF，BF=BC﹣FC，CE=BC﹣BE，

∴BF=CE，

在△ABF和△DCE中， ，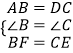

∴△ABF≌△DCE（SAS）；

（2）

证明：∵△ABF≌△DCE，

∴∠BAF=∠EDC，

∵∠DAF=90°﹣∠BAF，∠EDA=90°﹣∠EDC，

∴∠DAF=∠EDA，

∴△AOD是等腰三角形．

【解析】（1）根据矩形的性质可得∠B=∠C=90°，AB=DC，然后求出BF=CE，再利用“边角边”证明△ABF和△DCE全等即可；（2）根据全等三角形对应角相等可得∠BAF=∠EDC，然后求出∠DAF=∠EDA，然后根据等腰三角形的定义证明即可．
【考点精析】解答此题的关键在于理解等腰三角形的判定的相关知识，掌握如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等，以及对矩形的性质的理解，了解矩形的四个角都是直角，矩形的对角线相等．