
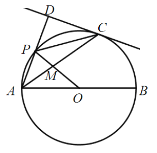
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,点
,点![]() 是
是![]() 上方圆上的一个动点,连接
上方圆上的一个动点,连接![]() ,作
,作![]() 的平分线
的平分线![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)当![]() _______时,四边形
_______时,四边形![]() 是平行四边形;
是平行四边形;
(3)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() _______时,
_______时,![]() 与
与![]() 相似.
相似.
【答案】(1)证明见解析;(2)2;(3)2或![]() .
.
【解析】
(1)易证∠PAC=∠ACO,从而可知AD∥OC,由于CD⊥AP,所以CD⊥OC,所以CD是⊙O的切线;
(2)根据一组对边平行且相等证得四边形![]() 是平行四边形;
是平行四边形;
(3)当△CDP∽△AMO时,则∠CDP=∠AMO=90°,利用等腰三角形AOC的三线合一可得∠AOP=∠COP,进而可证得AP=AO=2,当△CDP∽△AOM时,则∠CDP=∠AOP=90°,利用勾股定理可求得AP的长即可.
(1)证明:如图,连接![]() .
.

![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的切线.
的切线.
(2)当AP=2时,四边形![]() 是平行四边形,
是平行四边形,
理由如下:∵AP=2,OC=2,
∴AP=OC,
又∵AP∥OC,
∴四边形![]() 是平行四边形;
是平行四边形;
(3)如图,当△CDP∽△AMO时,则∠CDP=∠AMO=90°,
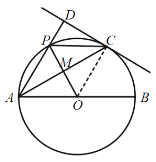
∴OP⊥AC,
又∵OA=OC,
∴∠AOP=∠COP,
∵AP∥OC,
∴∠APO=∠COP,
∴∠AOP=∠APO,
∴AP=AO=2,
当△CDP∽△AOM时,则∠CDP=∠AOP=90°,
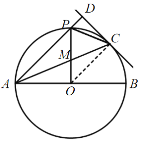
∵AO=PO=2,
∴在Rt△AOP中,AP=![]() ,
,
∴AP=2或![]()


科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 坐标为
坐标为![]() 轴上点
轴上点![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,过点
,过点![]() 作直线
作直线![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 直线
直线![]() 于
于![]() .
.
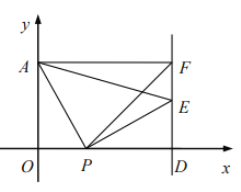
(1)当点![]() 是
是![]() 的中点时,求直线
的中点时,求直线![]() 的函数表达式.
的函数表达式.
(2)当![]() 时,求
时,求![]() 的面积.
的面积.
(3)在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,试用
?若存在,试用![]() 的代数式表示点
的代数式表示点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将如图所示的牌面数字1、2、3、4的四张扑克牌背面朝上,洗匀后放在桌面上.

(1)从中随机抽出一张牌,牌面数字是奇数的概率是 ;
(2)从中随机抽出两张牌,两张牌牌面数字的和是6的概率是 ;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用树状图或列表的方法求组成的两位数恰好是3的倍的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家医保局相关负责人3月25日表示,2019年底前我国将实现生育保险基金并入职工基本医疗保险基金,统一征缴,就是通常所说的“五险变四险”.传统的五险包括:养老保险、失业保险、医疗保险、工伤保险、生育保险.某单位从这五险中随机抽取两种,为员工提高保险比例,则正好抽中养老保险和医疗保险的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E,若CD=5,CE=4,则⊙O的半径是( )
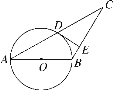
A.3B.4C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.
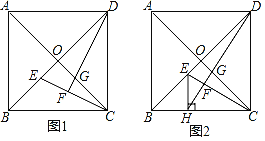
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AC:y=![]() x+8与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A,C,且与x轴的另一交点为B,又点P是抛物线的对称轴l上一动点.若△PAC周长的最小值为10+2
x+8与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A,C,且与x轴的另一交点为B,又点P是抛物线的对称轴l上一动点.若△PAC周长的最小值为10+2![]() ,则抛物线的解析式为_____.
,则抛物线的解析式为_____.
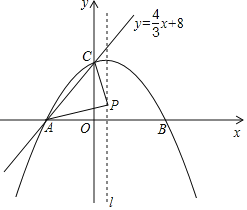
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,A、C分别在y轴、x轴上,且OA=6cm,OC=8cm,点P从点A开始以2cm/s的速度向B运动,点Q从点B开始以1cm/s的速度向C运动,设运动时间为t.
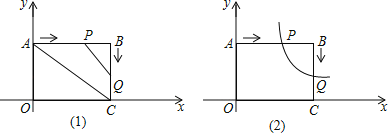
(1)如图(1),当t为何值时,△BPQ的面积为4cm2?
(2)当t为何值时,以B、P、Q为顶点的三角形与△ABC相似?
(3)如图(2),在运动过程中的某一时刻,反比例函数y=![]() 的图象恰好同时经过P、Q两点,求这个反比例函数的解析式.
的图象恰好同时经过P、Q两点,求这个反比例函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com