
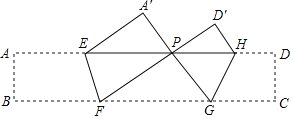
【题目】如图,把矩形ABCD沿EF,GH折叠,使点B,C落在AD上同一点P处,∠FPG=90°,△A′EP的面积是8![]() ,△D′PH的面积是4
,△D′PH的面积是4![]() ,则矩形ABCD的面积等于_____.
,则矩形ABCD的面积等于_____.
【答案】8(3![]() +2
+2![]() )
)
【解析】
由翻折可得∠A′=∠FPG,所以得A′E∥PF,可以证明△AE′P∽△D′PH,根据相似三角形面积的比等于相似比的平方可求得A′E=![]() D′P,再根据△A′EP的面积是8
D′P,再根据△A′EP的面积是8![]() 可求A′P=D′P=4,从而AE=A′E=4
可求A′P=D′P=4,从而AE=A′E=4![]() ,再根据勾股定理求得PE的长,进而求得D′H、PH,所以得AD=AE+EP+PH+DH,最后求得矩形ABCD的面积.
,再根据勾股定理求得PE的长,进而求得D′H、PH,所以得AD=AE+EP+PH+DH,最后求得矩形ABCD的面积.
解:由翻折可知:
∠A=∠A′=90°,∠D=∠D′=90°,
∵∠FPG=90°,
∴∠A′=∠FPG,
∴A′E∥PF,
∴∠A′EP=∠D′PH,
∴△AE′P∽△D′PH,
∴![]() ,
,
∵AB=CD,AB=A′P,CD=D′P,
∴A′P=D′P,
∵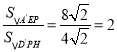 ,
,
∴A′E=![]() D′P,
D′P,
∴S△A′EP=![]() A′EA′P=
A′EA′P=![]() ×
×![]() D′PD′P=8
D′PD′P=8![]() ,
,
解得D′P=4(负值舍去),
∴A′P=D′P=4,
∴AE=A′E=4![]() ,
,
∴EP=![]() ,
,
∴PH=![]()
DH=D′H=![]() 2
2![]() ,
,
∴AD=AE+EP+PH+DH
=4![]() +4
+4![]()
![]() +2
+2![]()
=6![]() +4
+4![]() +2
+2![]() .
.
AB=A′P=4,
∴S矩形ABCD=ABAD
=4(6![]() +4
+4![]() +2
+2![]() )
)
=8(3![]() +2
+2![]() +
+![]() ).
).
故答案为:8(3![]() +2
+2![]() ).
).


科目:初中数学 来源: 题型:
【题目】 如图1,已知水龙头喷水的初始速度v0可以分解为横向初始速度vx和纵向初始速度vy,θ是水龙头的仰角,且v02=vx2+vy2.图2是一个建在斜坡上的花圃场地的截面示意图,水龙头的喷射点A在山坡的坡顶上(喷射点离地面高度忽略不计),坡顶的铅直高度OA为15米,山坡的坡比为![]() .离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为d=vyt-5t2;M与A的水平距离为vxt米.已知该水流的初始速度v0为15米/秒,水龙头的仰角θ为53°.
.离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为d=vyt-5t2;M与A的水平距离为vxt米.已知该水流的初始速度v0为15米/秒,水龙头的仰角θ为53°.

(1)求水流的横向初始速度vx和纵向初始速度vy;
(2)用含t的代数式表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围);
(3)水流在山坡上的落点C离喷射点A的水平距离是多少米?若要使水流恰好喷射到坡脚B处的小树,在相同仰角下,则需要把喷射点A沿坡面AB方向移动多少米?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小峰和小轩用两枚质地均匀的骰子做游戏,规则如下:每人随机掷两枚骰子一次(若掷出的两枚骰子摞在一起,则重掷),点数和大的获胜;点数和相同为平局.
依据上述规则,解答下列问题:
(1)随机掷两枚骰子一次,用列表法或树状图法求点数和为10的概率;
(2)小峰先随机掷两枚骰子一次,点数和是10,求小轩随机掷两枚骰子一次,胜小峰的概率.(骰子:六个面分别有1、2、3、4、5、6个小圆点的立方块.点数和:两枚骰子朝上的点数之和.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有两个相同的小球,它们分别写有1和2;乙口袋中装有三个相同的小球,它们分别写有3、4和5;丙口袋中装有两个相同的小球,它们分别写有6和7.从这3个口袋中各随机地取出1个小球.
(1)取出的3个小球上恰好有两个偶数的概率是多少?
(2)取出的3个小球上全是奇数的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
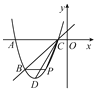
【题目】如图,已知抛物线y=ax2+bx+5经过A(-5,0),B(-4,-3)两点,与x轴的另一个交点为C,顶点为D,连接CD.
(1)求该抛物线的解析式;
(2)点P为该抛物线上一动点(与点B,C不重合),设点P的横坐标为t.当点P在直线BC的下方运动时,求△PBC的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
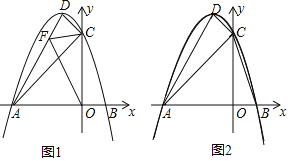
【题目】已知抛物线y=ax2+bx+3与x轴分别交于点A(﹣3,0),B(1,0)交于点C,抛物线的顶点为点D.
(1)抛物线的表达式及顶点D的坐标.
(2)若点F是线段AD上一个动点,
①如图1,当FC+FO的值最小时,求点F的坐标;
②如图2,以点A,F,O为顶点的三角形能否与△ABC相似?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 己知抛物线![]() 向右平移2个单位,再向下平移3个单位后恰好经过点
向右平移2个单位,再向下平移3个单位后恰好经过点![]() .
.
(1)求平移后抛物线的解析式;
(2)点A在平移后物线上,点A在该抛物线对称轴的右侧,将点A绕着原点逆时针旋转90°得到点B,设点A的横坐标为t;
①用t表示点B的坐标;
②若直线![]() ,且
,且![]() 与平移后抛物线只有一个交点C,当点
与平移后抛物线只有一个交点C,当点![]() 到直线AC距离取得最大值时,此时直线AC解析式.
到直线AC距离取得最大值时,此时直线AC解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于以AB为直径的⊙O,过点A作⊙O的切线,与BC的延长线相交于点D,在CB上截取CE=CD,连接AE并延长,交⊙O于点F,连接CF.
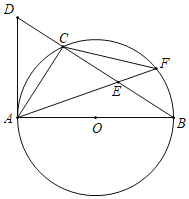
(1)求证:AC=CF;
(2)若AB=4,sinB![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,连接AC,O是AC的中点,M是AD上一点,且MD=1,P是BC上一动点,则PM﹣PO的最大值为_____.
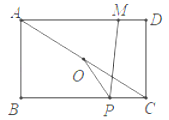
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com