
����Ŀ�� ��ͼ1����֪ˮ��ͷ��ˮ�ij�ʼ�ٶ�v0���Էֽ�Ϊ�����ʼ�ٶ�vx�������ʼ�ٶ�vy������ˮ��ͷ�����ǣ���v02=vx2+vy2��ͼ2��һ������б���ϵĻ��Գ��صĽ���ʾ��ͼ��ˮ��ͷ�������A��ɽ�µ��¶��ϣ�����������߶Ⱥ��Բ��ƣ����¶���Ǧֱ�߶�OAΪ15�ף�ɽ�µ��±�Ϊ![]() ���뿪ˮ��ͷ���ˮ�����ɵ㣩��ó�ʼ�ٶ�v0��/�����˶�·�����Կ����������ߣ���M���˶������е�ijһλ�ã����Կ���������ʵ�������M��A�ĸ߶�֮��d���ף������ʱ��t���룩�Ĺ�ϵΪd=vyt-5t2��M��A��ˮƽ����Ϊvxt�ף���֪��ˮ���ij�ʼ�ٶ�v0Ϊ15��/�룬ˮ��ͷ��������Ϊ53����
���뿪ˮ��ͷ���ˮ�����ɵ㣩��ó�ʼ�ٶ�v0��/�����˶�·�����Կ����������ߣ���M���˶������е�ijһλ�ã����Կ���������ʵ�������M��A�ĸ߶�֮��d���ף������ʱ��t���룩�Ĺ�ϵΪd=vyt-5t2��M��A��ˮƽ����Ϊvxt�ף���֪��ˮ���ij�ʼ�ٶ�v0Ϊ15��/�룬ˮ��ͷ��������Ϊ53����

��1����ˮ���ĺ����ʼ�ٶ�vx�������ʼ�ٶ�vy��
��2���ú�t�Ĵ���ʽ��ʾ��M�ĺ�����x��������y������y��x�Ĺ�ϵʽ����дx��ȡֵ��Χ����
��3��ˮ����ɽ���ϵ����C�������A��ˮƽ�����Ƕ����ף���Ҫʹˮ��ǡ�����䵽�½�B����С��������ͬ�����£�����Ҫ�������A������AB�����ƶ������ף����ο����ݣ�sin53���![]() ��cos53���
��cos53���![]() ��tan53���
��tan53���![]() ��
��
���𰸡���1��ˮ���ĺ����ʼ�ٶ�vx��9��/�룬�����ʼ�ٶ�vy��12��/�룻��2��y=-![]() +
+![]() x+15����3��ˮ����ɽ���ϵ����C�������A��ˮƽ������27�ף���Ҫ�������A������AB�����ƶ�
x+15����3��ˮ����ɽ���ϵ����C�������A��ˮƽ������27�ף���Ҫ�������A������AB�����ƶ�![]() ��
��
��������
��1���������������������Һ����Ҷ���ɵý��ۣ�
��2���ɣ�1���ı�ʾ��vx��ʾ��x��OA��֪������y=d+OA������OA��ֵ��d��t�ĺ�����ϵʽ�����Եý⣻
��3������õ�A�͵�B�����꣬����д����ֱ�߽���ʽ���ٽ����루2���������߽���ʽ�������Ӷ�������C�����꣬������ƽ��֪ʶ�����ɶ���������⣮
�⣺��1����v0Ϊ15��/�룬ˮ��ͷ��������Ϊ53����
��cos��=![]() ��sin��=
��sin��=![]() ��
��
��vx=15cos53��=15��![]() =9��vy=15sin53��=15��
=9��vy=15sin53��=15��![]() =12��
=12��
��ˮ���ĺ����ʼ�ٶ�vx��9��/�룬�����ʼ�ٶ�vy��12��/�룻
��2��x=vxt=9t��
��t=![]() ��
��
��M��A�ĸ߶�֮��d���ף������ʱ��t���룩�Ĺ�ϵΪd=vyt-5t2
��y=d+OA=12t-5t2+15=-5��![]() +12��
+12��![]() +15=-
+15=-![]() +
+![]() x+15��
x+15��
��y��x�Ĺ�ϵʽΪ��y=-![]() +
+![]() x+15��
x+15��
��3�����¶���Ǧֱ�߶�OAΪ15�ף�ɽ�µ��±�Ϊ![]() ��
��
��OB=45�ף���A��0��15����B��45��0��
��ֱ��AB�Ľ���ʽΪ��y=![]() +15�������������߽���ʽ�����ã�
+15�������������߽���ʽ�����ã�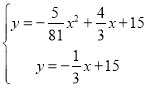 ��
��
���![]() ���ᣩ��
���ᣩ��![]() ��
��
��ˮ����ɽ���ϵ����C����Ϊ��27��6���������A������AB�����ƶ��ľ������BC�ľ��룬
��BC=![]() =
=![]() �ף�
�ף�
��ˮ����ɽ���ϵ����C�������A��ˮƽ������27�ף���Ҫ�������A������AB�����ƶ�![]() �ף�
�ף�


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����Ͳ�����������ʽ��������Ա�����ʶ�ȡ�ͣ������˷����ù�˾����10�����ţ��Ҹ����ŵ�������ͬ.Ϊ�˽���͵��˷����������10�������������ȡ��![]() �������ţ��������������ܣ�20�������գ��ĵ��飬�õ�����������ÿ������˷ѷ��˵����������¼����ÿ�ղ�������������λ��ǧ�ˣ���������Щ���ݽ����������������ͷ���.��������˲�����Ϣ.
�������ţ��������������ܣ�20�������գ��ĵ��飬�õ�����������ÿ������˷ѷ��˵����������¼����ÿ�ղ�������������λ��ǧ�ˣ���������Щ���ݽ����������������ͷ���.��������˲�����Ϣ.![]() .
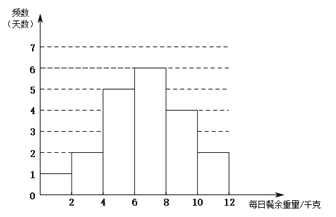
.![]() ����ÿ�ղ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺
����ÿ�ղ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺![]() ��
��![]() ��
��![]() ��
��![]() ����
����
![]() .
.![]() ����ÿ�ղ���������
����ÿ�ղ���������![]() ��һ����ǣ�6.1 6.6 7.0 7.0 7.0 7.8
��һ����ǣ�6.1 6.6 7.0 7.0 7.0 7.8
![]() .
.![]() ����ÿ�ղ����������£�1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
����ÿ�ղ����������£�1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
![]() .
. ![]() ����������20��������ÿ�ղ���������ƽ��������λ�����������£�
����������20��������ÿ�ղ���������ƽ��������λ�����������£�
���� | ƽ���� | ��λ�� | ���� |
| 6.4 | | 7.0 |
| 6.6 | 7.2 | |
����������Ϣ���ش��������⣺
��1��д����![]() �е�ֵ��
�е�ֵ��
��2����![]() �����������У����ʶ�ȡ�ͣ������˷������ýϺõIJ�����________������
�����������У����ʶ�ȡ�ͣ������˷������ýϺõIJ�����________������![]() ������
������![]() ������������____________��
������������____________��
��3�����![]() ����������ÿ�ղ������������ݣ����Ƹù�˾��10�����ţ�һ�꣨��240�������ռ��㣩�IJ���������.
����������ÿ�ղ������������ݣ����Ƹù�˾��10�����ţ�һ�꣨��240�������ռ��㣩�IJ���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����мף������ֻ����˶�����������ij����������װ����ϼ��ͻ����˱����ͻ�����ÿСʱ�ٰ���30ǧ�ˣ����ͻ����˰���600ǧ�����õ�ʱ�������ͻ����˰���800ǧ�����õ�ʱ����ͬ�����ֻ�����ÿСʱ�ֱ���˶���ǧ�ˣ�����ͻ�����ÿСʱ����xǧ�ˣ��������⣬���з���Ϊ(����)
A. ![]() ��
��![]() B.
B. ![]() ��
��![]()
C. ![]() ��
��![]() D.
D. ![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ���Ż��������ƶ��ն˵�Ѹ�ٷ�չ�����ֻ��Ķ�Խ��Խ�ռ��� �����������ϵġ���ͷ�塱Խ��Խ�࣬ij�о�������ԡ�����ο������ֻ��Ķ����������������ʾ����飨�ʾ�ѵ�������ͼ��ʾ�����������������Ƴ�ͼ�ٺ�ͼ����ʾ��ͳ��ͼ��������������
������ο����̻��Ķ����ʾ������
���ã�����һ�ݹ���������ο������ֻ�����ʵ���������ڱ�����ѡ��һ�������Ϲ۵㣬�����ո��ڴ��������dz���л���ĺ�����
���Ż��������ƶ��ն˵�Ѹ�ٷ�չ�����ֻ��Ķ�Խ��Խ�ռ��� �����������ϵġ���ͷ�塱Խ��Խ�࣬ij�о�������ԡ�����ο������ֻ��Ķ����������������ʾ����飨�ʾ�ѵ�������ͼ��ʾ�����������������Ƴ�ͼ�ٺ�ͼ����ʾ��ͳ��ͼ��������������
������ο����̻��Ķ����ʾ������
���ã�����һ�ݹ��ڡ�����ο������ֻ�������ʵ���������ڱ�����ѡ��һ�������Ϲ۵㣬�����ո��ڴ��������dz���л���ĺ�����
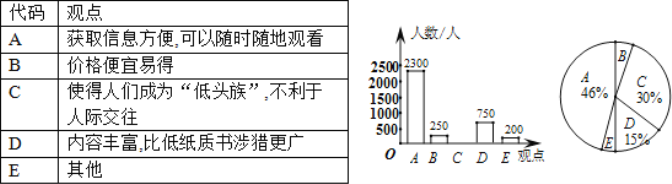
�����ͳ��ͼ���ṩ����Ϣ������������⣺
��1�����ν��ܴʲ����������______�ˣ���������ͳ��ͼ����������
��2��������ͳ��ͼ�У��۵�E�İٷֱ���_______����ʾ�۵�B�����ε�Բ�ĽǶ���Ϊ______�ȣ�
��3��ij�й���300���ˣ���������ϵ�����������г�![]() �۵������ֻ��Ķ����������ж������ˣ�
�۵������ֻ��Ķ����������ж������ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧΪ��չ��У�Ƽ���������ƻ�����A�͡�B�������ͺŵĺ�ģ��������8��A�ͺ�ģ��5��B�ͺ�ģ����2200Ԫ��������4��A�ͺ�ģ��6��B�ͺ�ģ����1520Ԫ����A��B�����ͺź�ģ�ĵ��۷ֱ��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij�߲���ֲũ������ײ�����������繲1000�꣬���аײ���ÿ��3Ԫ����������ÿ��5Ԫ����֪��ũ�������ò�����3600Ԫ��������3800Ԫ���ʽ��������߲ˣ�
��1�����ũ�����Թ���ײ������������ֵ����Сֵ��
��2����ũ������1���й���ײ�����������Сֵ�ķ������������߲��磬����ũ���ľ��������������߲���ȫ�ɻ�������������ݷ�����ƽ��һ��ײ���ɳ���2ǧ�˰ײˣ�ƽ��һ����������ɽ�3ǧ����������ũ���ƻ�����ֱ�����ۺ���̬��ժ�������ַ�ʽ�������ۣ�����ֱ�����۰ײ˵��ۼ�Ϊÿǧ��4Ԫ��ֱ���������������ۼ�Ϊÿǧ��5Ԫ����̬��ժ����ʱ�����߲˵��ۼ�һ��������ֱ�����۰ײ˵��ۼ۸�![]() ������̬��ժ�����л���
������̬��ժ�����л���![]() ����ģ����ײ˺���������ֱ������һ���ʣ�µ�ȫ��������̬��ժ����ʱ����ũ���ɻ��8080Ԫ��������
����ģ����ײ˺���������ֱ������һ���ʣ�µ�ȫ��������̬��ժ����ʱ����ũ���ɻ��8080Ԫ��������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
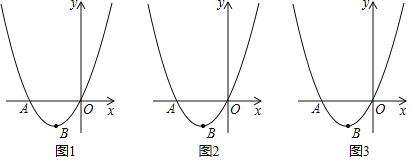
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+bx��x�ύ�ڵ�A������B������Ϊ����2����2����
��1����a��b��ֵ��
��2����y����������ȡ��C��0��4�����ڵ�A�������������һ��P������PB��x���ڵ�D������CB��x���ڵ�F����CBƽ�֡�DCOʱ�����P�����ꣻ
��3���ڣ�2���������£�����PC����PB����һ��E������EC������ECB����PDC�����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
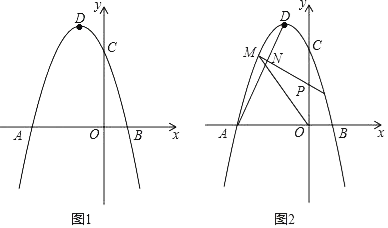
����Ŀ����ͼ�������ߵĶ���D������Ϊ����1��4������������x���ཻ��A��B���㣨A��B����ࣩ����y�ύ�ڵ�C��0��3����
��1���������ߵı���ʽ��
��2����ͼ1����֪��E��0����3�����������ߵĶԳ������Ƿ����һ��F��ʹ����CEF���ܳ���С��������ڣ������F�����ꣻ��������ڣ���˵�����ɣ�
��3����ͼ2������AD������P���߶�OC�ϵ�һ���㣬����P���߶�AD�Ĵ��ߣ��ڵڶ����ֱ��������ߡ��߶�AD�ཻ�ڵ�M��N����MN���ʱ������POM�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
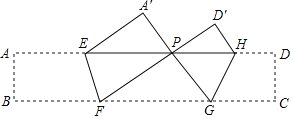
����Ŀ����ͼ���Ѿ���ABCD��EF��GH�۵���ʹ��B��C����AD��ͬһ��P������FPG��90������A��EP�������8![]() ����D��PH�������4
����D��PH�������4![]() �������ABCD���������_____��
�������ABCD���������_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com