
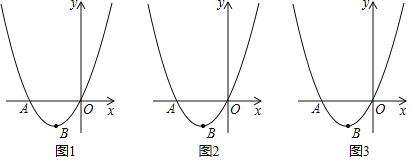
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于点A,顶点B的坐标为(﹣2,﹣2).
(1)求a,b的值;
(2)在y轴正半轴上取点C(0,4),在点A左侧抛物线上有一点P,连接PB交x轴于点D,连接CB交x轴于点F,当CB平分∠DCO时,求点P的坐标;
(3)在(2)的条件下,连接PC,在PB上有一点E,连接EC,若∠ECB=∠PDC,求点E的坐标.
【答案】(1)a=![]() ,b=2;(2)P(﹣6,6);(3)(﹣
,b=2;(2)P(﹣6,6);(3)(﹣![]() ,
,![]() )
)
【解析】
(1)根据顶点B的坐标及原点即可求出解析式;
(2)过点B作BH⊥y轴于点H,过点D作DG⊥CB于点G,先求出tan∠BCH=![]() ,再根据CB平分∠DCO求出点D的坐标,得到直线BD的解析式,利用抛物线的解析式即可得到点P的坐标;
,再根据CB平分∠DCO求出点D的坐标,得到直线BD的解析式,利用抛物线的解析式即可得到点P的坐标;
(3)过点P作PM⊥y轴于点M,过点B作BH⊥y轴于点H,证明△PMC≌△CHB得到∠CPB=∠CBP=45°,过点C作CN⊥CE,过点B作BN⊥BP,CN、BN交于点N,连接DN,证明△ECD≌△NCD得到DE=DN,过点P作PK⊥x轴于点K,利用勾股定理求出PD,设ED=t,作BQ⊥x轴于点Q,求出BD后根据勾股定理求出ED,作ER⊥x轴于点R,根据平行线所截线段成比例求出ER,再根据三角函数求出DR即可得到点E的坐标.
解:(1)抛物线的表达式为:y=a(x+2)2﹣2=ax2+4ax+4a﹣2,
故4a﹣2=0,
解得:a=![]() ,
,
b=4a=2;
(2)抛物线的表达式为:y=![]() x2+2x…①,
x2+2x…①,
过点B作BH⊥y轴于点H,过点D作DG⊥CB于点G,
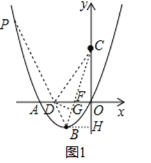
由点B、C的坐标得直线BC的表达式为:y=3x+4,则点F(﹣![]() ,0),
,0),
∵点B(﹣2,﹣2),BH=2,CH=4+2=6,则tan∠BCH=![]() =tanα,
=tanα,
∵DG⊥BC,
∴∠FDG=∠FCO=α=∠DCG,
在Rt△DFG中,设FG=m,则DG=3m,
则CG=3DG=9m,
CF=9m﹣m=8m=![]() ,
,
解得:m=![]() ,
,
DF=![]() ,
,
OD=OF+DF=3,故点D(﹣3,0),
由点B、D的坐标可得,直线PB的表达式为:y=﹣2x﹣6…②,
联立①②并解得:x=﹣2(舍去)或﹣6,
故点P(﹣6,6);
(3)如图2,过点P作PM⊥y轴于点M,过点B作BH⊥y轴于点H,
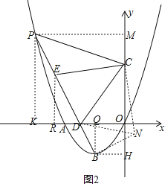
∵P(﹣6,6),
则PM=OM=6,
∴CM=2,PM=CH,
∴BH=CM,
∵∠PMC=∠BHC=90°,
∴△PMC≌△CHB(HL),
∴CP=CB,∠MPC=∠BCH,
∵∠MPC+∠PCM=90°,
∴∠BCH+∠PCM=90°,
∴∠PCB=90°,
∴∠CPB=∠CBP=45°,
过点C作CN⊥CE,过点B作BN⊥BP,CN、BN交于点N,连接DN,
则∠CBN=90°﹣∠CPB=45°,
∴∠CPB=∠CBN,
∵∠ECN=∠EBN=90°,
∴∠CEB+∠CNB=180°,
∵∠CEB+∠PEC=180°,
∴∠CNB=∠PEC,
∵PC=CB,
∴△PEC≌△BNC(SAS),
则PE=BN,CE=CN,
∵∠ECB=∠EDC+∠DCB,∠PDC=∠DCB+∠CBD,∠ECB=∠PDC,
∴∠ECD=∠CBD=45°,
∴∠DCN=90°﹣∠ECD=45°,
∴∠ECD=∠DCN,
∵CD=CD,
∴△ECD≌△NCD(SAS),
∴DE=DN,
在Rt△DBN中,BD2+BN2=DN2,则BD2+PE2=DE2,
过点P作PK⊥x轴于点K,
∴PK=KO=6,
∵OD=3,
∴KD=3,
在Rt△PKD中,PD=![]() ,
,
设ED=t,则PE=3![]() ﹣t,
﹣t,
过点B作BQ⊥x轴于点Q,则BQ=OQ=2,DQ=OD﹣OQ=1,
在Rt△BDQ中,BD=![]() =
=![]() ,
,
故(![]() )2+(3
)2+(3![]() ﹣t)2=t2,
﹣t)2=t2,
解得:t=![]() ,
,
故DE=![]() ,
,
过点E作ER⊥x轴于点R,则ER∥PK,
故![]() ,即
,即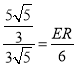 ,
,
解得:ER=![]()
∵∠EDR=∠BDQ,
故tan∠EDR=tan∠BDQ,
即:![]() =2,
=2,
故DR=![]() ,OR=DR+OD=
,OR=DR+OD=![]() +3=
+3=![]() ,
,
故点E的坐标为:(﹣![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
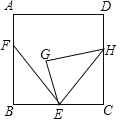
【题目】如图,正方形 ABCD 中,点 E,F 分别在 BC 和 AB 上,BE=3,AF=2,BF=4,将△ BEF 绕点 E 顺时针旋转,得到△GEH,当点 H 落在 CD 边上时,F,H 两点之间的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
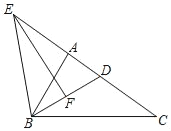
【题目】已知:如图,在△ABC中,点D在边AC上,BD的垂直平分线交CA的延长线于点E,交BD于点F,联结BE,ED2=EAEC.
(1)求证:∠EBA=∠C;
(2)如果BD=CD,求证:AB2=ADAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图1,已知水龙头喷水的初始速度v0可以分解为横向初始速度vx和纵向初始速度vy,θ是水龙头的仰角,且v02=vx2+vy2.图2是一个建在斜坡上的花圃场地的截面示意图,水龙头的喷射点A在山坡的坡顶上(喷射点离地面高度忽略不计),坡顶的铅直高度OA为15米,山坡的坡比为![]() .离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为d=vyt-5t2;M与A的水平距离为vxt米.已知该水流的初始速度v0为15米/秒,水龙头的仰角θ为53°.
.离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为d=vyt-5t2;M与A的水平距离为vxt米.已知该水流的初始速度v0为15米/秒,水龙头的仰角θ为53°.

(1)求水流的横向初始速度vx和纵向初始速度vy;
(2)用含t的代数式表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围);
(3)水流在山坡上的落点C离喷射点A的水平距离是多少米?若要使水流恰好喷射到坡脚B处的小树,在相同仰角下,则需要把喷射点A沿坡面AB方向移动多少米?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种进价为每件10元的日用商品,经调查发现,该商品每天的销售量![]() (件)与销售单价
(件)与销售单价![]() (元)满足
(元)满足![]() ,设销售这种商品每天的利润为
,设销售这种商品每天的利润为![]() (元).
(元).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在保证销售量尽可能大的前提下,该商场每天还想获得2000元的利润,应将销售单价定为多少元?
(3)当每天销售量不少于50件,且销售单价至少为32元时,该商场每天获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
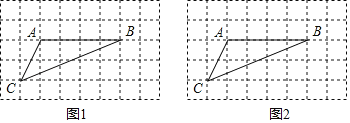
【题目】如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画出△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且四边形ACBD是中心对称图形;
(2)在图2中找一点E(点E在小正方形的顶点上),使tan∠AEB=2(AE<EB),且四边形ACEB的对边不平行,并直接写出图2中四边形ACEB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
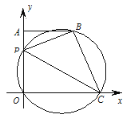
【题目】如图,在平面直角坐标系中,A(0,4),B(3,4),P 为线段 OA 上一动点,过 O,P,B 三点的圆交 x 轴正半轴于点 C,连结 AB, PC,BC,设 OP=m.
(1)求证:当 P 与 A 重合时,四边形 POCB 是矩形.
(2)连结 PB,求 tan∠BPC 的值.
(3)记该圆的圆心为 M,连结 OM,BM,当四边形 POMB 中有一组对边平行时,求所有满足条件的 m 的值.
(4)作点 O 关于 PC 的对称点O ,在点 P 的整个运动过程中,当点O 落在△APB 的内部 (含边界)时,请写出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小峰和小轩用两枚质地均匀的骰子做游戏,规则如下:每人随机掷两枚骰子一次(若掷出的两枚骰子摞在一起,则重掷),点数和大的获胜;点数和相同为平局.
依据上述规则,解答下列问题:
(1)随机掷两枚骰子一次,用列表法或树状图法求点数和为10的概率;
(2)小峰先随机掷两枚骰子一次,点数和是10,求小轩随机掷两枚骰子一次,胜小峰的概率.(骰子:六个面分别有1、2、3、4、5、6个小圆点的立方块.点数和:两枚骰子朝上的点数之和.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 己知抛物线![]() 向右平移2个单位,再向下平移3个单位后恰好经过点
向右平移2个单位,再向下平移3个单位后恰好经过点![]() .
.
(1)求平移后抛物线的解析式;
(2)点A在平移后物线上,点A在该抛物线对称轴的右侧,将点A绕着原点逆时针旋转90°得到点B,设点A的横坐标为t;
①用t表示点B的坐标;
②若直线![]() ,且
,且![]() 与平移后抛物线只有一个交点C,当点
与平移后抛物线只有一个交点C,当点![]() 到直线AC距离取得最大值时,此时直线AC解析式.
到直线AC距离取得最大值时,此时直线AC解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com