
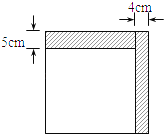
【题目】如图,小明将一个正方形纸剪去一个宽为![]() 的长条后, 再从剩下的长方形纸片上剪去一个宽为
的长条后, 再从剩下的长方形纸片上剪去一个宽为![]() 的长条,如果两次剪下的长条面积正好相等,那么剩下的白色长方形纸的面积为( )
的长条,如果两次剪下的长条面积正好相等,那么剩下的白色长方形纸的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
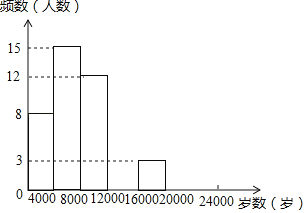
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
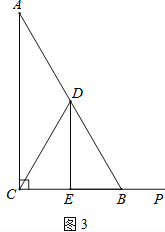
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 ;
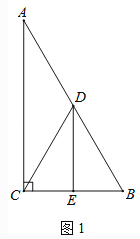
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
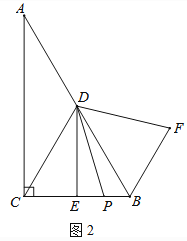
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
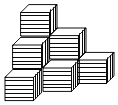
【题目】棱长为a的正方体,摆放成如图所示的形状,动手试一试,并回答下列问题:
(1)如果这一物体摆放了如图所示的上下三层,由几个正方体构成?
(2)如图形所示物体的表面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学将组织七年级学生春游一天,由王老师和甲、乙两同学到客车租赁公司洽谈租车事宜.
(1)两同学向公司经理了解租车的价格,公司经理对他们说:“公司有45座和60座两种型号的客车可供租用,60座的客车每辆每天的租金比45座的贵100元.”王老师说:“我们学校八年级昨天在这个公司租了5辆45座和2辆60座的客车,一天的租金为1600元,你们能知道45座和60座的客车每辆每天的租金各是多少元吗”甲、乙两同学想了一下,都说知道了价格.
聪明的你知道45座和60座的客车每辆每天的租金各是多少元吗?
(2)公司经理问:“你们准备怎样租车”,甲同学说:“我的方案是只租用45座的客车,可是会有一辆客车空出30个座位”;乙同学说“我的方案只租用60座客车,正好坐满且比甲同学的方案少用两辆客车”,王老师在﹣旁听了他们的谈话说:“从经济角度考虑,还有别的方案吗”?如果是你,你该如何设计租车方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=-![]() x+2与x轴、y轴分别交于点A、C,抛物线y=-
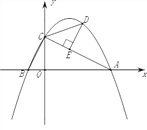
x+2与x轴、y轴分别交于点A、C,抛物线y=-![]() x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作
x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作![]() 于点E.
于点E.
(1)求抛物线的表达式;
(2)求△ACD面积的最大值;
(3)若△CED与△COB相似,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com