
分析 (1)观察已知等式,得到拆项规律,写出即可;
(2)利用得出的规律将原式变形,计算即可得到结果;
(3)原式利用程序法变形,计算即可得到结果.
解答 解:(1)根据题意得:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{1007}$-$\frac{1}{1008}$=1-$\frac{1}{1008}$=$\frac{1007}{1008}$;
(3)原式=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{2014}$-$\frac{1}{2016}$)=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{2016}$)=$\frac{1007}{4032}$.
故答案为:(1)$\frac{1}{n}$-$\frac{1}{n+1}$;(2)$\frac{1007}{1008}$
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
| x(支) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3x+5(10-x)(元) | 48 | 46 | 44 | 42 | 40 | 38 | 36 | 34 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
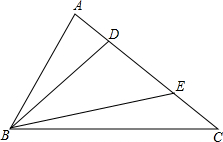 已知△ABC中.∠ABC=60°,D、E为边AC上的两点.DE=4,BD=6,BE=8.∠ABD=20°,∠CBE=10°,试在边AB、BC上分别找一点F、G.使四边形DFGE的周长最短.
已知△ABC中.∠ABC=60°,D、E为边AC上的两点.DE=4,BD=6,BE=8.∠ABD=20°,∠CBE=10°,试在边AB、BC上分别找一点F、G.使四边形DFGE的周长最短.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com