
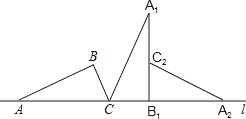
【题目】如图,把直角△ABC的斜边AC放在直线l上,按顺时针的方向在直线l上转动两次,使它转到△A2B1C2的位置,设AB=![]() ,∠BAC=30°,则顶点A运动到点A2的位置时,点A所经过的路线为( )
,∠BAC=30°,则顶点A运动到点A2的位置时,点A所经过的路线为( )
A. ( ![]() +
+![]() )π B. (
)π B. (![]() +
+![]() )π C. 2π D.
)π C. 2π D. ![]() π
π
 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,—抛物线y=﹣a(x+1)(x﹣3)(a>0)与x轴交于A、B两点,与y轴交于点C.抛物线的对称轴与x轴交于点E,过点C作x轴的平行线,与抛物线交于点D,连接DE,延长DE交y轴于点F,连接AD、AF.
(1)点A的坐标为____________,点B的坐标为_________ ;
(2)判断四边形ACDE的形状,并给出证明;
(3)当a为何值时,△ADF是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“厨余垃圾”的概率;
(2)求小丽投放的两袋垃圾不同类的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
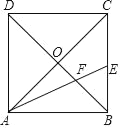
【题目】如图,正方形ABCD的边长为![]() +1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
+1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
(1)求证:△ABF∽△ACE;
(2)求tan∠BAE的值;
(3)在线段AC上找一点P,使得PE+PF最小,求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
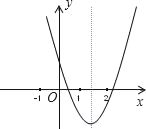
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
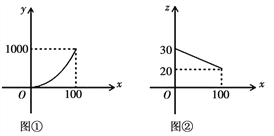
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用![]() 万元
万元![]() 与年产量
与年产量![]() 万件
万件![]() 之间的函数图象是顶点为原点的抛物线的一部分
之间的函数图象是顶点为原点的抛物线的一部分![]() 如图
如图![]() 所示
所示![]() ;该产品的销售单价
;该产品的销售单价![]() 元
元![]() 件
件![]() 与年销售量
与年销售量![]() 万件
万件![]() 之间的函数图象是如图
之间的函数图象是如图![]() 所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元
所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元![]() 毛利润
毛利润![]() 销售额
销售额![]() 生产费用
生产费用![]()
![]() 请写出y与x以及z与x之间的函数关系式;
请写出y与x以及z与x之间的函数关系式;
![]() 求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字:![]() ,1,2,
,1,2,![]() 的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法![]() 只选其中一种
只选其中一种![]() ,表示两次抽出卡片上的数字的所有结果;
,表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点![]() 落在双曲线
落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com