
����Ŀ������ͬѧ����������һ�����⣺��ͼ1��ʾ����֪AF��BE�ǡ�ABC�����ߣ���AF��BE������ΪP����BC=a��AC=b��AB=c��
��֤��a2+b2=5c2
��ͬѧ��ϸ�����õ����½���˼·��
������EF������EFΪ��ABC����λ�ߵõ���EPF�ס�BPA���� ![]() ����PF=m��PE=n����m��n��PA��PB�ֱ��ʾ����������Rt��APE��Rt��BPF�����ù��ɶ������㣬��ȥm��n���ɵ�֤
����PF=m��PE=n����m��n��PA��PB�ֱ��ʾ����������Rt��APE��Rt��BPF�����ù��ɶ������㣬��ȥm��n���ɵ�֤
��1������������Ͻ���˼·������ͬѧд��֤�����̣�
��2���������еĽ��ۣ�����������⣺�ڱ߳�Ϊ3������ABCD�У�OΪ�Խ���AC��BD�Ľ��㣬E��F�ֱ�Ϊ�߶�AO��DO���е㣬����BE��CF���ӳ����ڵ�M��BM��CM�ֱ�AD�ڵ�G��H����ͼ2��ʾ����MG2+MH2��ֵ��
���𰸡�
��1��
�⣺��PF=m��PE=n������EF����ͼ1��
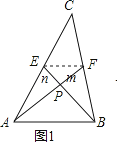
��AF��BE�ǡ�ABC�����ߣ�
��EFΪ��ABC����λ�ߣ�AE= ![]() b��BF=
b��BF= ![]() a��
a��
��EF��AB��EF= ![]() c��
c��
���EFP�ס�BPA��
�� ![]() ����
���� ![]() =
= ![]() ��
��
��PB=2n��PA=2m��
��Rt��AEP����PE2+PA2=AE2��
��n2+4m2= ![]() b2�٣�
b2�٣�
��Rt��AEP����PF2+PB2=BF2��
��m2+4n2= ![]() a2�ڣ�
a2�ڣ�
��+�ڵ�5��n2+m2��= ![]() ��a2+b2����
��a2+b2����
��Rt��EFP����PE2+PF2=EF2��
��n2+m2=EF2= ![]() c2��
c2��
��5 ![]() c2=
c2= ![]() ��a2+b2����
��a2+b2����
��a2+b2=5c2��
��2��
�⣺���ı���ABCDΪ���Σ�
��BD��AC��
��E��F�ֱ�Ϊ�߶�AO��DO���е㣬
�ɣ�1���Ľ��۵�MB2+MC2=5BC2=5��32=45��
��AG��BC��
���AEG�ס�CEB��
�� ![]() =
= ![]() ��
��
��AG=1��
ͬ���ɵ�DH=1��
��GH=1��
��GH��BC��
�� ![]() =
= ![]() ��
��
��MB=3GM��MC=3MH��
��9MG2+9MH2=45��
��MG2+MH2=5��
����������1����PF=m��PE=n������EF����ͼ1��������������λ�����ʵ�EF��AB��EF= ![]() c������жϡ�EFP�ס�BPA���������Ʊȵõ�PB=2n��PA=2m�����Ÿ��ݹ��ɶ����õ�n2+4m2=
c������жϡ�EFP�ס�BPA���������Ʊȵõ�PB=2n��PA=2m�����Ÿ��ݹ��ɶ����õ�n2+4m2= ![]() b2 �� m2+4n2=
b2 �� m2+4n2= ![]() a2 �� ��5��n2+m2��=
a2 �� ��5��n2+m2��= ![]() ��a2+b2������n2+m2=EF2=
��a2+b2������n2+m2=EF2= ![]() c2 �� ����a2+b2=5c2����2�����ã�1���Ľ��۵�MB2+MC2=5BC2=5��32=45�������á�AEG�ס�CEB�ɼ����AG=1��ͬ���ɵ�DH=1����GH=1��Ȼ������GH��BC������ƽ���߷��߶γ����������õ�MB=3GM��MC=3MH��Ȼ�����������ɵ�MG2+MH2=5�����⿼�������������ε��ж���ƽ���������ε�һ�ߵ�ֱ�������������ཻ�������ɵ���������ԭ���������ƣ�������Ƕ�Ӧ��ȵ��������������ƣ�Ҳ��������������λ�����ʺ����ε����ʣ�
c2 �� ����a2+b2=5c2����2�����ã�1���Ľ��۵�MB2+MC2=5BC2=5��32=45�������á�AEG�ס�CEB�ɼ����AG=1��ͬ���ɵ�DH=1����GH=1��Ȼ������GH��BC������ƽ���߷��߶γ����������õ�MB=3GM��MC=3MH��Ȼ�����������ɵ�MG2+MH2=5�����⿼�������������ε��ж���ƽ���������ε�һ�ߵ�ֱ�������������ཻ�������ɵ���������ԭ���������ƣ�������Ƕ�Ӧ��ȵ��������������ƣ�Ҳ��������������λ�����ʺ����ε����ʣ�


 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ涨����Сѧ��ÿ����У�����ʱ�䲻����1Сʱ��Ϊ�˽��������ߵ���ʵ������йز��ž͡���ij����У�����ʱ���Ƕ��١������⣬��ijУ�������˲���ѧ�����ٸ��ݻʱ��t��Сʱ�����з��飨A�飺t��0.5��B�飺0.5��t��1��C�飺1��t��1.5��D�飺t��1.5�������Ƴ���������������ͳ��ͼ�������ͼ����Ϣ�ش����⣺
��1���˴γ���ѧ����Ϊ�ˣ�
��2����ȫ����ͳ��ͼ��
��3���ӳ���ѧ�������ѯ��һ��ѧ��������������У�����ʱ�����1Сʱ�ĸ�����
��4����������Уѧ����Ϊ1200�ˣ�������ڵ���ﵽ���ҹ涨�����ʱ���ѧ�����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ϴ������ϵġ���Ȼ¥����������������һ¥����ijУ��ѧ���ŵ�ͬѧ�Գ�Ȼ¥�ĸ߶Ƚ����˲�������ͼ��������A�������������������Ϊ30�㣬����¥�ķ���ǰ��60m��B�����������Ϊ60�㣬��ѧ�������ߺ��Բ��ƣ� ![]() ��1.7�������ȷ��1m�����¥�ĸ߶�CDΪ�� ��
��1.7�������ȷ��1m�����¥�ĸ߶�CDΪ�� �� 
A.47m
B.51m
C.53m
D.54m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB�Ļƽ�ָ�㣨AC��BC�������н��۴�����ǣ� ��![]()
A.![]()
B.BC2=AB?BC
C.![]() ��
��![]()
D.![]() ��0.618
��0.618
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���A=90�㣬AB=AC �� BC=63cm�����صױ����δ������ϲü����Ⱦ�Ϊ3cm�ľ���ֽ������ͼ��ʾ����֪���õ�ֽ������һ���������Σ�������������ֽ���Ǵ������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߳�Ϊ4cm��������ABCD�����Ķ���A��ת180�㣬����B��������·�߳�Ϊ cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪԭ�㣬��A��4��0������B��0��3�����ѡ�ABO�Ƶ�B��ʱ����ת���á�A��BO�䣬��A��O��ת��Ķ�Ӧ��ΪA�䣬O�䣬����ת��Ϊ����
��1����ͼ�٣�����=90�㣬��AA��ij���
��2����ͼ�ڣ�����=120�㣬���O������ꣻ
��3���ڣ��������£���OA�� ��һ��P��ת��Ķ�Ӧ��ΪP�䣬��O��P+BP��ȡ����Сֵʱ�����P������ֱ꣨��д��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɫ���У���̼�������ѳ�Ϊ�������Ĺ�ʶ��ij���ξ���������һ���������г�ͣ������6��00��18��00������ڴ˽������г���Ҳ�ɽ��ڸ�ͣ�������õ����г����ڴ˵أ��ֻ�ͬѧͳ����������ͣ������ʱ�εĽ衢�����г������Լ�ͣ��������ʱ�̵����г���������Ϊ�����������������x=1ʱ��yֵ��ʾ7��00ʱ�Ĵ�����x=2ʱ��yֵ��ʾ8��00ʱ�Ĵ������������ƣ������ִ���y��������x��xΪ������������ͼ��ʾ��һ�����κ�����ϵ�� 
ʱ�� | x | ������ | �賵�� | ����y |
6��00��7��00 | 1 | 45 | 5 | 100 |
7��00��8��00 | 2 | 43 | 11 | n |
�� | �� | �� | �� | �� |
��������ͼ����Ϣ������������⣺
��1��m= �� ����m��ʵ�����壺��
��2��������ʱ�̵����г�����y��x֮������Ķ��κ�����ϵʽ��
��3����֪9��00��10��O0���ʱ�εĻ������Ƚ賵����3����4�����ʱ�εĽ賵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬���ۡ�C��ʹ��C����б��AB��ijһ��D�����ۺ�ΪEF����E��F�ֱ��ڱ�AC��BC�ϣ��� 
��1������C��E��FΪ���������������A��B��CΪ��������������ƣ� �ٵ�AC=BC=2ʱ��AD�ij�Ϊ��
�ڵ�AC=3��BC=4ʱ��AD�ij�Ϊ��
��2������D��AB���е�ʱ����CEF���CBA��������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com