
如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为 .

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
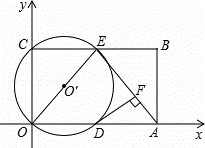
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)由已知可得,△ AOE是等腰三角形.那么直线BC
AOE是等腰三角形.那么直线BC
上存不存在除点E以外的点P,使△AOP也是等腰三角
形?如果不存在,说明理由;如果存在,直接写出P点
的坐标.
 |
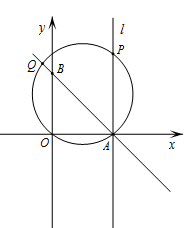
查看答案和解析>>
科目:初中数学 来源: 题型:
从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
| 种子粒数 | 100 | 400 | 800 | 1 000 | 2 000 | 5 000 |
| 发芽种子粒数 | 85 | 398 | 652 | 793 | 1 604 | 4 005 |
| 发芽频率 | 0.850 | 0.745] | 0.851 | 0.793 | 0.802 | 0.801 |
根据以上数据可以估计,该玉米种子发芽的概率约为 (精 确到0.1).
确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )
A.  B.
B. 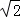 ﹣1 C. 2﹣
﹣1 C. 2﹣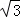 D.
D. 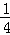
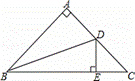
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q,已知⊙O的直径为10,tan∠ABC= ,则CQ最大值为( )
,则CQ最大值为( )
A.5 B. C.
C.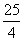 D.
D.
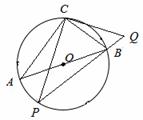
查看答案和解析>>
科目:初中数学 来源: 题型:
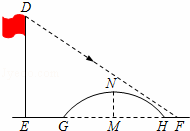
如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=ax2+bx+c(a≠0)的图象经过一次函数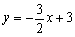 的图象与x轴、y轴的交点,并也经过(1,1)点.求这个二次函数解析式,并求x为何值时,有最大(最小)值,这个值是什么?
的图象与x轴、y轴的交点,并也经过(1,1)点.求这个二次函数解析式,并求x为何值时,有最大(最小)值,这个值是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
以边长为1的正方形ABCD的顶点A为圆心,以 为半径作⊙A,则点C关于⊙
为半径作⊙A,则点C关于⊙ A的位置关系是( )
A的位置关系是( )
A. 点C 在⊙A内 B. 点C在⊙A上 C. 点C在⊙A外 D. 不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com