
����Ŀ��ѧУ������Ҫȥ�̵깺��Ǧ�ʺ���Ƥ��������60֧Ǧ�ʺ�30����Ƥ�����谴���ۼ۹���֧��30Ԫ��������90֧Ǧ�ʺ�60����Ƥ����ɰ������۹���֧��40.5Ԫ����֪ÿ֧Ǧ�ʵ������۱����ۼ۵�0.05Ԫ��ÿ����Ƥ�������۱����ۼ۵�0.10Ԫ��
��1����ÿ֧Ǧ�ʺ�ÿ����Ƥ�������۸��Ƕ���Ԫ��
��2��С��ͬѧ��4ԪǮ������̵갴���ۼ���ͬ����Ǧ�ʺ���Ƥ��������Ҫ��4ԪǮǡ�����꣩�������ļ��ֹ�����
���𰸡���1��ÿ֧Ǧ�ʵ�������Ϊ0.25Ԫ��ÿ����Ƥ��������Ϊ0.3Ԫ����2��С���������ֹ���
��������
��1����ÿ֧Ǧ�ʵ�������ΪxԪ��ÿ����Ƥ��������ΪyԪ��������������60֧Ǧ�ʺ�30����Ƥ�����谴���ۼ۹���֧��30Ԫ��������90֧Ǧ�ʺ�60����Ƥ����ɰ������۹���֧��40.5Ԫ�������ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2������Թ���m֧Ǧ�ʣ�n����Ƥ�������ܼۣ����������������ɵó�����m��n�Ķ�Ԫһ�η��̣��ٽ��m��n��Ϊ���������ɵó���������
��1����ÿ֧Ǧ�ʵ�������ΪxԪ��ÿ����Ƥ��������ΪyԪ��
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
��ÿ֧Ǧ�ʵ�������Ϊ0.25Ԫ��ÿ����Ƥ��������Ϊ0.3Ԫ��
��2������Թ���m֧Ǧ�ʣ�n����Ƥ��
�����⣬�ã���0.25+0.05��m+��0.3+0.1��n��4��
��n��10��![]() m��
m��
��m��n����������
��![]() ��
��![]() ��
��![]() ��
��
��С���������ֹ���������1������4֧Ǧ�ʣ�7����Ƥ������2������8֧Ǧ�ʣ�4����Ƥ������3������12֧Ǧ�ʣ�1����Ƥ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��b���dz�������k��0����ͼ���㣨1��0���ͣ�0��2����
��1������2��x��3ʱ����y��ȡֵ��Χ��
��2����֪��P��m��n���ڸú�����ͼ���ϣ���m��n=4�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ס��ҡ��������ִ��Ӹۿ�O���������ֱ���ʻ��A��B��C��ʱ���������ã��״�λ�ڸۿڵı�ƫ��43��45�������Ҵ�λ�ڸۿڵı�ƫ��76��35��������λ�ڸۿڵı�ƫ��43��45������
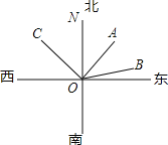
��1������BOC�Ķ�����
��2������AOB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,���ı���ABCD��,AD��BC,��AD>BC,BC=6 cm,����P,Q�ֱ��A,Cͬʱ����,P��1 cm/s���ٶ���A��D�˶�,Q��2cm/s���ٶ���C��B�˶�(Q�˶���Bʱ����ͬʱֹͣ�˶�),��________���ı���ABQPΪƽ���ı���.
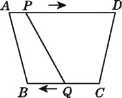
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ���и���A(��1��0)����A��1����������1����λ����A1(��1��1)�������ŵ�2����������2����λ����A2(1��1)����3����������1����λ����A3����4����������3����λ����A4����5������������1����λ����A5����6����������4����λ����A6�����������˹���������ȥ����A��2019����������A2019��������____��
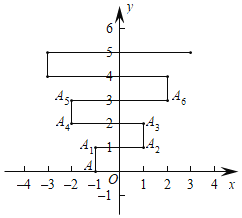
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� �Ķ�����
����1����֪a��b��c��dΪ������![]() ��ac=bd����˵��a=d��b=c.
��ac=bd����˵��a=d��b=c.
����ͨ�����켸��ģ�ͽ����������. ע�����![]() �������a��b��c��d�ֱ���Ϊ����ֱ�������ε�ֱ�DZߣ���ô�ɹ���ͼ1��ʾ�ļ���ģ��.
�������a��b��c��d�ֱ���Ϊ����ֱ�������ε�ֱ�DZߣ���ô�ɹ���ͼ1��ʾ�ļ���ģ��.
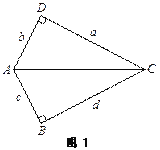
��ac=bd,
��AB��CD=BC��AD
��![]()
���㰴������˼·�������˵��.
�� ����̽��
����2����a��0��b��0���ԱȽ�![]() ��
��![]() �Ĵ�С.
�Ĵ�С.
Ϊ�����ǹ���ͼ2��ʾ�ļ���ģ�ͣ�����ABΪֱ��, OΪԲ�ģ���C�ڰ�Բ�ϣ�CD��AB ��D��AD��a��BD��b.
��������ͼ2��ʾ�ļ���ģ�ͽ�����������2��
�� ��չ����
���ں���y=x+![]() ����x��0ʱ����y��ȡֵ��Χ��
����x��0ʱ����y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʦ�ڽ���ʵ����ʱ����һ��ͼ(��ͼ)������������ĵ�λ����Ϊ����һ�������Σ�Ȼ����ԭ��ΪԲ�ģ������εĶԽ��߳�Ϊ�뾶�����������ڵ�A.

(1)A���ʾ�����Ƕ���?�������ϣ�A�����ʾһ1.42�ĵ���ʲôλ�ù�ϵ;
(2)����Ϊ��ʦ��������ͼ��Ϊ��˵��ʲô?
(3)���������������������ϻ�����ʾ-![]() �ĵ�B.(�뱣����ͼ�ۼ�)
�ĵ�B.(�뱣����ͼ�ۼ�)
�鿴�𰸺ͽ���>>
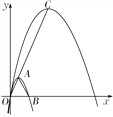
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������C1��y����![]() x2��2
x2��2![]() x�Ķ���ΪA����x��������ύ�ڵ�B.
x�Ķ���ΪA����x��������ύ�ڵ�B.
(1)��������C1�ϵĵ�ĺ�����������궼����ԭ����2������任��õ��������ߵı���ʽ��
(2)��������C1�ϵĵ�(x��y)��Ϊ(kx��ky)(|k|��1)���任��õ�����������C2��������C2�Ķ���ΪC����������C2�ı���ʽ(��k��ʾ)��
(3)��(2)�����£���P��������C2�ϣ�����S��PAC��S��ABC���ҡ�ACP��90��.��k��1ʱ����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲�����ֱ���AB�ĸ߶���ij�ۺ�ʵ��С���ڵ���D����ֱ���ñ��CD�����ڵ�����ˮƽ���ø�ƽ�澵E��ʹ��B��E��D��ͬһˮƽ��������ͼ��ʾ.��С���ڱ�˵�F��ͨ��ƽ�澵Eǡ�ù۲��˶�A(��ʱ��AEB=��FED).��F�������˶�A������Ϊ39.3�㣬ƽ�澵E�ĸ���Ϊ45�㣬FD=1.8���������AB�ĸ߶�ԼΪ������? (�����������)(�ο�������tan39.3���0.82��tan84.3���10.02)

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com