
【题目】已知:如图,直线y=x﹣15与x轴、y轴分别相交于点A和点B.抛物线![]() 经过A、B两点.
经过A、B两点.
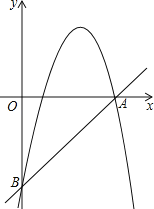
(1)求这个抛物线的解析式;
(2)若这抛物线的顶点为点D,与x轴的另一个交点为点C.对称轴与x轴交于点H,求△DAC的面积;
(3)若点E是线段AD的中点.CE与DH交于点G,点P在y轴的正半轴上,△POH是否能够与△CGH相似?如果能,请求出点P的坐标;如果不能,请说明理由.
【答案】(1)y=﹣![]() x2+6x﹣15;(2)△DAC的面积为72;(3)△POH能够与△CHG相似,相似时点P的坐标为P1(0,6)或P2(0,
x2+6x﹣15;(2)△DAC的面积为72;(3)△POH能够与△CHG相似,相似时点P的坐标为P1(0,6)或P2(0,![]() ).
).
【解析】
(1)利用一次函数的解析式,求得A、B的坐标,再代入抛物线得出方程组,即可求出抛物线的解析式;
(2)分别求出点D、点C的坐标,根据三角形的面积公式即可求得答案;
(3)根据题目的条知点G是△DAC的重心,首先求得![]() 的值,再根据相似三角形的性质得出两个比例式,代入即可求得点P的坐标.
的值,再根据相似三角形的性质得出两个比例式,代入即可求得点P的坐标.
(1)∵y=x﹣15,
y=0时,0=x﹣15,
∴x=15,
当x=0时,y=﹣15,
∴A(15,0),B(0,﹣15),
代入得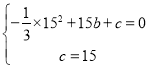 ,
,
解得![]() ,
,
∴抛物线的解析式:![]() .
.
(2)抛物线的解析式可变形为![]() ,
,
∴顶点D坐标为(9,12),
设y=0,则![]() ,
,
∴(x﹣9)2=36.
∴x1=3,x2=15,
∴点C的坐标为(3,0),
∴![]() .
.
(3)∵点E是线段AD的中点,点H是线段AC的中点,.
∴点G是△DAC的重心.如图:
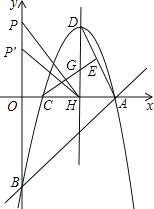
∵顶点D坐标为(9,12),
∴![]() ,
,
∴HO=9,CH=6.
设△POH∽△GHC时,
![]() ,
,
∴![]()
∴PO=6,
∴P1(0,6);
△POH∽△CHG时,![]() ,
,
![]() ,
,
∴![]() .
.
∴![]() .
.
∴△POH能够与△CHG相似,相似时点P的坐标为P1(0,6)或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】四张小卡片上分别写有数字-1,1,2,3,它们除数字外没有任何区别,现将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字2的概率;
(2)随机地从盒子里抽取一张,将数字记为![]() ,不放回再抽取第二张,将数字记为
,不放回再抽取第二张,将数字记为![]() ,请你用画树状图或列表的方法表示所有等可能的结果,并求出点
,请你用画树状图或列表的方法表示所有等可能的结果,并求出点![]() 在函数
在函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数![]() 的图像与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
的图像与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是__________________
的自变量x的取值范围是__________________
(2)如表示y与x的几组对应值:
x | … |
|
|
|
|
|
|
|
|
|
|
| … |
y | … |
|
|
|
|
|
|
|
|
|
| m | … |
表中m的值为____________
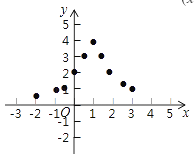
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数![]() 的大致图像;
的大致图像;
(4)结合函数图像,请写出函数![]() 的2条性质:
的2条性质:
①__________________________________________________________________________
②__________________________________________________________________________
(5)解决问题:如果函数![]() 与直线
与直线![]() 的交点有2个,那么a的取值范围是_______________________
的交点有2个,那么a的取值范围是_______________________
(6)![]() 在函数图像上,若
在函数图像上,若![]() ,则m的取值范围______________
,则m的取值范围______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校基础教育杂志社在我校九年级学生中开展征文活动,征文主题只能从“爱国”、“敬业”、“诚信”、“友善”四个主題中选择一个,九年级每名学生按要求都上交了一份征文,学校为了了解选择各种征文主题的学生人数.随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图:
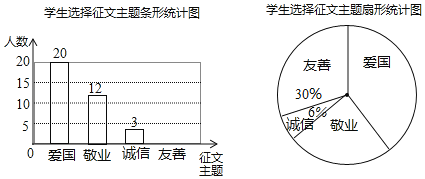
(1)本次调查共抽取了多少名学生的征文,并将上面的条形统计图补充完整;
(2)这次调查的四个主题的“众数”为 ;
(3)如果我校九年级共有1500名学生,请估计选择以“友善”为主题的九年级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有着辉煌的数学成就,《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.
(1)小聪想从这4部数学名著中随机选择1部阅读,求他选中《九章算术》的概率;
(2)小聪拟从这4部数学名著中选择2部作为假课外拓展学习内容,用列表或树状图求选中的名著恰好是《九章算术》和《周牌算经》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D在BC边上(不与B、C重合),在AC上取一点E,使∠ADE=30°.
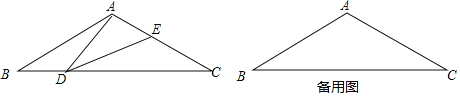
(1)求证:△ABD∽△DCE;
(2)若BD=n(0<n<2![]() ),求线段AE的长;(用含n的代数式表示)
),求线段AE的长;(用含n的代数式表示)
(3)当△ADE是等腰三角形时,请直接写出AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
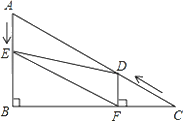
【题目】如图,在Rt△ABC中,∠B=90°,BC=5![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com