
【题目】(7分)如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 在第一象限
在第一象限
的图象交于![]() 点,过
点,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,已知
,已知![]() 的面积为1.
的面积为1.
(1)求反比例函数的解析式;
(2)如果![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点![]() 与点
与点![]() 不重合),且
不重合),且![]() 点的横坐标为1,在
点的横坐标为1,在![]() 轴上求一点
轴上求一点![]() ,使
,使![]() 最小.
最小.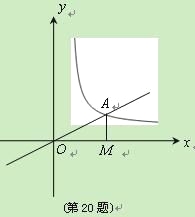
【答案】解:(1)设![]() 点的坐标为(
点的坐标为(![]() ,
,![]() ),则
),则![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴反比例函数的解析式为![]() .··································································· 3分
.··································································· 3分
(2) 由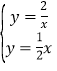 得
得![]() ∴
∴![]() 为(
为(![]() ,
,![]() ). ·············································· 4分
). ·············································· 4分
设![]() 点关于
点关于![]() 轴的对称点为
轴的对称点为![]() ,则
,则![]() 点的坐标为(
点的坐标为(![]() ,
,![]() ).
).
令直线![]() 的解析式为
的解析式为![]() .
.
∵![]() 为(
为(![]() ,
,![]() )∴
)∴![]() ∴
∴![]()
∴![]() 的解析式为
的解析式为![]() .···································································· 6分
.···································································· 6分
当![]() 时,
时,![]() .∴
.∴![]() 点为(
点为(![]() ,
,![]() ). ······················································ 7分
). ······················································ 7分
【解析】
试题(1)设出A点的坐标,然后根据△OAM的面积为1,确定出k的值即可;(2)分别求出点A、B的坐标以及点A关于![]() 轴的对称点C的坐标,然后求出直线BC的解析式,直线BC与x轴的交点即为所求.
轴的对称点C的坐标,然后求出直线BC的解析式,直线BC与x轴的交点即为所求.
试题解析:(1)设A点的坐标为(![]() ,
,![]() ),
),
则![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴反比例函数的解析式为![]() .
.
(2) 由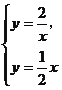 得
得![]() 或
或![]() ∴A为
∴A为![]() .
.
设A点关于![]() 轴的对称点为C,则C点的坐标为
轴的对称点为C,则C点的坐标为![]() .
.
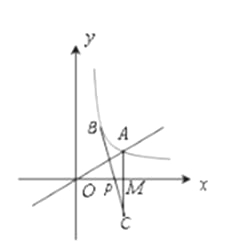
如要在![]() 轴上求一点P,使PA+PB最小.则P点应为BC和x轴的交点,如图所示.
轴上求一点P,使PA+PB最小.则P点应为BC和x轴的交点,如图所示.
令直线BC的解析式为![]() .
.
∵B为(![]() ,
,![]() ),∴
),∴![]() ∴
∴![]()
∴BC的解析式为![]() .
.
当![]() 时,
时,![]() .∴P点坐标为
.∴P点坐标为 .
.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】某企业1~5月份利润的变化情况图所示,以下说法与图中反映的信息相符的是( )
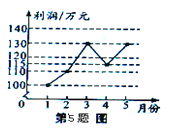
A. 1~2月份利润的增长快于2~3月份分利润的增长
B. 1~4月份利润的极差与1~5月份利润的极差不同
C. 1~5月份利润的的众数是130万元
D. 1~5月份利润的中位数为120万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的顶点A、B、D均在⊙O上,请仅用无刻度的直尺按要求作图.
(1)AB边经过圆心O,在图(1)中作一条与AD边平行的直径; 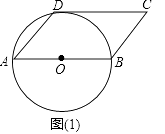
(2)AB边不经过圆心O,DC与⊙O相切于点D,在图(2)中作一条与AD边平行的弦. 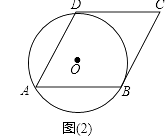
查看答案和解析>>
科目:初中数学 来源: 题型:
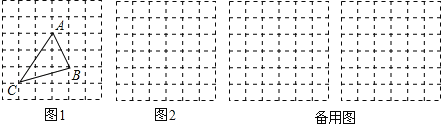
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在两个不透明的口袋中分别装有三个颜色分别为红色、白色、绿色的小球,这三个小球除颜色外其他都相同,
(1)在其中一个口袋中一次性随机摸出两个球,请写出在这一过程中的一个必然事件;
(2)若分别从两个袋中随机取出一个球,试求出两个小球颜色相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.
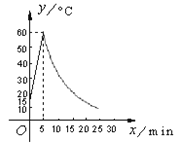
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com