
如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度,已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以15单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
【考点】一元一次方程的应用;数轴.
【分析】(1)设点A的速度为每秒t个单位,则点B的速度为每秒4t个单位,由甲的路程+乙的路程=总路程建立方程求出其解即可;
(2)设x秒时原点恰好在A、B的中间,根据两点离原点的距离相等建立方程求出其解即可;
(3)先根据追击问题求出A、B相遇的时间就可以求出C行驶的路程.
【解答】解:(1)设点A的速度为每秒t个单位,则点B的速度为每秒4t个单位,由题意,得
3t+3×4t=15,
解得:t=1,
则点A的速度为每秒1个单位长度,则点B的速度为每秒4个单位长度.
如图:
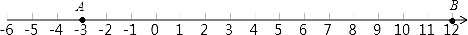
(2)设x秒时原点恰好在A、B的中间,由题意,得
3+x=12﹣4x,
解得:x=1.8.
则A、B运动1.8秒时,原点就在点A、点B的中间;
(3)由题意,得
B追上A的时间为:15÷(4﹣1)=5,
则C行驶的路程为:5×15=75单位长度.
【点评】本题考查了列一元一次方程解实际问题的运用,数轴的运用,行程问题的相遇问题和追及问题的数量关系的运用,解答时根据行程问题的数量关系建立方程是关键.


科目:初中数学 来源: 题型:
已知:多项式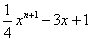 的次数的3.
的次数的3.
(1)填空: = ;
= ;
(2)直接判断:单项式 与单项式
与单项式 是否为同类项 (填“是”或“否”);
是否为同类项 (填“是”或“否”);
|
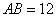 cm,点
cm,点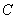 是直线
是直线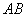 上一点,且
上一点,且 ·
·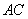 ,若点
,若点 是
是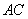 的中点,求线段
的中点,求线段 的长.
的长. 第26题图
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )
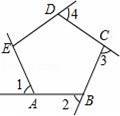

A.80° B.100° C.108° D.110°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com