练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

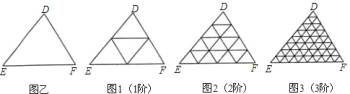
    【题目】一般地，“任意三角形都是自相似图形”，只要顺次连接三角形各边中点，则可将原三角形分割为四个都与它自己相似的小三角形．我们把（图乙）第一次顺次连接各边中点所进行的分割，称为阶分割（如图）；把阶分割得出的个三角形再分别顺次连接它的各边中点所进行的分割，称为阶分割（如图）…，依此规则操作下去．阶分割后得到的每一个小三角形都是全等三角形（为正整数），设此时小三角形的面积为．请写出一个反映，，之间关系的等式________．

    【答案】

    【解析】

    1阶三角形有4个，把这4个三角形再分，每个分成4个，即共有42个三角形，即2阶三角形有42个三角形，进而可以得到n阶三角形有4n个三角形．

    解：设△DEF的面积是a
    则Sn-1=，Sn=，Sn+1=

    根据()2=

    因而Sn-1，Sn，Sn+1三者之间关系式是Sn2=Sn-1Sn+1．

    ∴三者之间关系式是Sn2=Sn-1Sn+1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，已知点D在线段AB的反向延长线上，过AC的中点F作线段GE交∠DAC的平分线于E，交BC于G，且AE∥BC．

    （1）求证：△ABC是等腰三角形；

    （2）若AE＝8，AB＝10，GC＝2BG，求△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，六边形ABCDEF∽六边形GHIJKL，相似比为2：1，则下列结论正确的是（ ）

    A. ∠E=2∠K B. BC=2HI C. 六边形ABCDEF的周长=六边形GHIJKL的周长 D. S六边形ABCDEF=2S六边形GHIJKL

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，光明中学一教学楼顶上竖有一块高为AB的宣传牌，点E和点D分别是教学楼底部和外墙上的一点(A，B，D，E在同一直线上)，小红同学在距E点9米的C处测得宣传牌底部点B的仰角为67°，同时测得教学楼外墙外点D的仰角为30°，从点C沿坡度为1∶的斜坡向上走到点F时，DF正好与水平线CE平行．

    (1)求点F到直线CE的距离(结果保留根号)；

    (2)若在点F处测得宣传牌顶部A的仰角为45°，求出宣传牌AB的高度(结果精确到0.01)．(注：sin67°≈0.92，tan67°≈2.36，≈1.41，≈1.73)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程x2﹣（2m+1）x+m（m+1）=0，

    （1）求证：方程总有两个不相等的实数根；

    （2）设方程的两根分别为x1、x2，求的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了促进节能减排，倡导节约用电，某市将实行居民生活用电阶梯电价方案，图中折线反映了每户每月用电电费y（元）与用电量x（度）间的函数关系式．

    （1）根据图象，阶梯电价方案分为三个档次，填写下表：

    档次

    第一档

    第二档

    第三档

    每月用电量x（度）

    0＜x≤140



    （2）小明家某月用电120度，需交电费 元

    （3）求第二档每月电费y（元）与用电量x（度）之间的函数关系式；

    （4）在每月用电量超过230度时，每多用1度电要比第二档多付电费m元，小刚家某月用电290度，交电费153元，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（基础运用）

    如图①所示，直线L：y=x+5与x轴负半轴，y轴正半轴分别交于A、B两点．

    （1）点A坐标为 ，S△OAB= ；

    （2）如图②所示，设Q为AB延长线上一点，作直线OQ，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，①求证：△AOM≌△OBN；②若AM=4，求MN的长；

    （思维延伸）直线L：y=mx+5m与x轴负半轴，y轴正半轴分别交于A、B两点．

    （3）当m取不同的值时，点B在y轴正半轴上运动，分别以OB、AB为边，点B为直角顶点在第 一、二象限内作等腰直角△OBF和等腰直角△ABE，连EF交y轴于P点，如图③．问：当点B在y轴正半轴上运动时，试猜想线段PE与线段PF的数量关系并证明；

    （4）如图③，当m取不同的值时，点B在y轴正半轴上运动，以AB为边在第二象限作等腰直角△ABE，则动点E在直线 上运动.（直接写出直线的表达式）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：E在△ABC的AC边的延长线上，D点在AB边上，DE交BC于点F，DF=EF，BD=CE。求证：△ABC是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=ax2+bx+c的图象过点A（3，0），对称轴为直线x=1，给出以下结论：①abc＜0；②b2﹣4ac＞0；③a+b+c≥ax2+bx+c；④若M（x2+1，y1）、N（x2+2，y2）为函数图象上的两点，则y1＜y2，其中正确的是（　　）

    A. ①②③ B. ①②④ C. ①③④ D. ②③④

    查看答案和解析>>

    同步练习册答案