
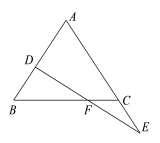
【题目】如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE。求证:△ABC是等腰三角形.
【答案】证明见解析.
【解析】
过点D作DG∥AC交BC于点G,根据平行线的性质可得出∠GDF=∠E、∠DGB=∠ACB,结合DF=EF以及∠DFG=∠EFC可证出△GDF≌△CEF(ASA),根据全等三角形的性质可得出GD=CE,结合BD=CE可得出BD=GD,进而可得出∠B=∠DGB=∠ACB,由此即可证出△ABC是等腰三角形.
过点D作DG∥AC交BC于点G,如图所示.

∵DG∥AC,
∴∠GDF=∠E,∠DGB=∠ACB.
在△GDF和△CEF中,
 ,
,
∴△GDF≌△CEF(ASA),
∴GD=CE.
∵BD=CE,
∴BD=GD,
∴∠B=∠DGB=∠ACB,
∴AB=AC
∴△ABC是等腰三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与
与![]() 轴交点的横坐标为
轴交点的横坐标为![]() ,
,![]() ,则对于下列结论:
,则对于下列结论:
①当![]() 时,
时,![]() ;
;
②方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ;
;
③![]() .
.
其中正确的结论有________(只需填写序号即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
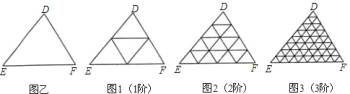
【题目】一般地,“任意三角形都是自相似图形”,只要顺次连接三角形各边中点,则可将原三角形分割为四个都与它自己相似的小三角形.我们把![]() (图乙)第一次顺次连接各边中点所进行的分割,称为
(图乙)第一次顺次连接各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() );把
);把![]() 阶分割得出的
阶分割得出的![]() 个三角形再分别顺次连接它的各边中点所进行的分割,称为
个三角形再分别顺次连接它的各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() )…,依此规则操作下去.
)…,依此规则操作下去.![]() 阶分割后得到的每一个小三角形都是全等三角形(
阶分割后得到的每一个小三角形都是全等三角形(![]() 为正整数),设此时小三角形的面积为
为正整数),设此时小三角形的面积为![]() .请写出一个反映
.请写出一个反映![]() ,
,![]() ,
,![]() 之间关系的等式________.
之间关系的等式________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,BE、CD相交于点O.

(1)若BD=CE,试说明:OB=OC.
(2)若BC=10,BC边上的中线AM=12,试求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰三角形ABC,∠A是顶角,且∠A等于∠C的一半,BD是△ABC的角平分线,则该图中共有等腰三角形的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
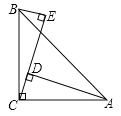
(1)直线BE与AD的位置关系是 ;BE与AD之间的距离是线段 的长;
(2) 若AD=6cm,BE=2cm.,求BE与AD之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列问题,列出关于![]() 的方程,并将其化成一元二次方程的一般形式.
的方程,并将其化成一元二次方程的一般形式.
(1)4个完全相同的正方形的面积之和是25,求正方形的边长![]() .
.
(2)一个矩形的长比宽多2,面积是100,求矩形的长![]() .
.
(3)一个直角三角形的斜边长为10,两条直角边相差2,求较长的直角边长![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com