Question

【题目】如图,△ABC中,∠BAC=60°,

(1)如果△ABC角平分线BD、CE相交与点O，则∠BOC_________。

(2)如果△ABC的高BD、CE相交与点O，求∠BOC的度数。

Answer 1

【答案】（1）=120；（2）∠BOC =120°.

【解析】

（1）根据三角形内角和定理和角平分线定义求出∠OBC+∠OCB的度数，然后在△BOC中通过三角形内角和定理可求出∠BOC的度数；

（2）由高线的定义可知∠AEC=90°，∠ADB=90°，然后根据四边形内角和定理可求出∠DOE，问题得解.

解（1）如图1，

∵∠BAC=60°，

∴∠ABC+∠ACB=180°-∠BAC=120°，

∵BD、CE分别是∠ABC，∠ACB的角平分线，

∴∠OBC=∠ABC，∠OCB=∠ACB，

∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ACB+∠ACB)=60°，

∴∠BOC=180°-(∠OBC+∠OCB)=120°；

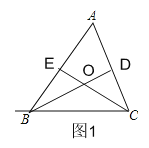
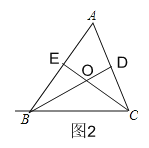
（2）如图2，

∵∠BAC=60°，BD、CE是△ABC的高线，

∴∠AEC=90°，∠ADB=90°，

∴∠DOE=360°-∠BAC-∠AEC-∠ADB=360°-60°-90°-90°=120°，

∴∠BOC=∠DOE=120°.