
分析 (1)用待定系数法求出抛物线的解析式,运用配方法求出对称轴和顶点坐标;
(2)根据点P(5,n)在抛物线上,求出点P的坐标,根据抛物线的对称性求出PE的长,根据梯形面积的求法求出四边形AOEP的面积.
解答 解:(1)由题意得,
$\left\{\begin{array}{l}{-16+4b+c=0}\\{-1+b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=4}\\{c=0}\end{array}\right.$,
∴该抛物线的表达式为:y=-x2+4x,
∵y=-x2+4x=-(x-2)2+4,
∴抛物线的对称轴是x=2,和顶点坐标(2,4);
(2)当x=5时,y=-5,∴点P(5,-5),
∵点P(5,-5)与点E关于x=2对称,∴PE=6,
又∵OA=4,
∴四边形AOEP的面积为:$\frac{1}{2}$(4+6)×5=25.
点评 本题考查的是待定系数法求二次函数的解析式和二次函数的性质,正确运用待定系数法是解题的关键,注意正确运用配方法求抛物线的对称轴和顶点坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| 数据x | 70<x<79 | 80<x<89 | 90<x<99 |
| 个数 | 800 | 1300 | 900 |
| 平均数 | 78.1 | 85 | 91.9 |
| A. | 92.16 | B. | 85.23 | C. | 84.73 | D. | 77.97 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
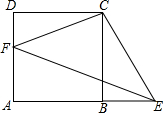 如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°
如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{(-8)^{2}}$=-8 | B. | (-$\sqrt{8}$)2=64 | C. | $\sqrt{(-25)^{2}}$=±25 | D. | $\sqrt{9\frac{1}{16}}$=3$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com