
分析 矩形ABCD对折后所得矩形与原矩形相似,则矩形ABCD∽矩形BFEA,设矩形的长为a,宽为b.则AB=CD=b,AD=BC=a,BF=AE=$\frac{a}{2}$,根据矩形相似,对应边的比相等得到比例式,计算即可.
解答 解:设矩形的长为a,宽为b,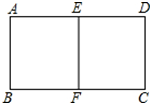
则AB=CD=b,AD=BC=a,BF=AE=$\frac{a}{2}$,
∵矩形ABCD∽矩形BFEA,
∴$\frac{AE}{AB}$=$\frac{AB}{AD}$,
即$\frac{\frac{a}{2}}{b}$=$\frac{b}{a}$,
∴a:b=$\sqrt{2}$:1.
故答案为:$\sqrt{2}$:1.
点评 本题考查的是相似多边形的性质,掌握相似多边形的对应边的比相等是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
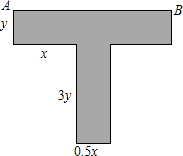 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | xy2(x-1)=x2y2-xy2 | B. | x2+x-5=(x-2)(x+3)+1 | C. | (a+3)(a-3)=a2-9 | D. | 2a2+4a=2a(a+2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com