
 如图,在正方形ABCD中,AB=12,E是AB边上一点,且AE=3BE,P是对角线AC上一动点,则PB+PE的最小值是15.
如图,在正方形ABCD中,AB=12,E是AB边上一点,且AE=3BE,P是对角线AC上一动点,则PB+PE的最小值是15. 分析 由正方形的性质可知;点B与点D关于AC对称,由轴对称的性质可知PB=PD,当点E、P、D在一条直线上时,PE+PB有最小值,最后根据勾股定理求得ED的长即可.
解答 解:如图所示:连接ED交AC与点P.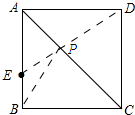
∵四边形ABCD是正方形,
∴点B与点D关于AC对称.
∴PB=PD.
∴PE+PB=PD+EP.
由两点之间线段最短可知:当点E、P、D在一条直线上时,PE+PB有最小值,最小值为ED.
在Rt△ADE中,ED=$\sqrt{A{D}^{2}+A{E}^{2}}$=15,
故答案为:15.
点评 本题主要考查的是正方形的性质、轴对称-路径最短问题、勾股定理,明确当点E、P、D在一条直线上时,PE+PB有最小值是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
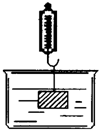 如图,在物理实验课上,小明用弹簧秤将铁块A从完全置身水槽外,到匀速向下放入盛有水的水槽中,直至铁块完全浸入水面下的一定深度,则图能反映弹簧秤的读数y(单位:N)与铁块下降的高度x(单位:cm)之间的函数关系的大致图象是( )
如图,在物理实验课上,小明用弹簧秤将铁块A从完全置身水槽外,到匀速向下放入盛有水的水槽中,直至铁块完全浸入水面下的一定深度,则图能反映弹簧秤的读数y(单位:N)与铁块下降的高度x(单位:cm)之间的函数关系的大致图象是( )| A. | 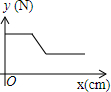 | B. | 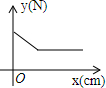 | C. | 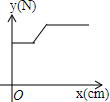 | D. | 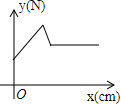 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
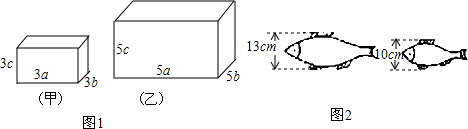
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a是任意实数 | B. | 与b,c的值有关 | C. | 与a的值有关 | D. | 与a的符号有关 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $x=\frac{{-2±\sqrt{5}}}{2}$ | B. | $x=\frac{{2±\sqrt{5}}}{2}$ | C. | $x=\frac{{1±\sqrt{5}}}{2}$ | D. | $x=\frac{{1±\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com