
����Ŀ����֪����ͼ1���߶�AB��CD�ཻ�ڵ�O������AD��CB�����ǰ�����ͼ1��ͼ�γ�֮Ϊ��8���Ρ����Խ���������⣺
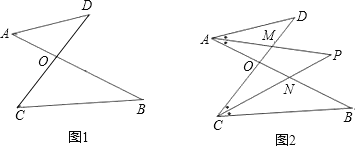
��1����ͼ1�У���ֱ��д����A����B����C����D֮���������ϵ�� ��
��2����ϸ�۲죬��ͼ2�С�8���Ρ��ĸ����� ����
��3����ͼ2�У�����D=40������B=36������DAB����BCD��ƽ����AP��CP�ཻ�ڵ�P��������CD��AB�ֱ��ཻ��M��N�����ã�1���Ľ��ۣ�������P�Ķ�����
��4�����ͼ2����D����BΪ�����ʱ�������������䣬������P����D����B֮�������������������ϵ����ֱ��д�����ۼ��ɣ�
���𰸡���1����A+��D=��B+��C��2��6��3��38����4��2��P=��B+��D
��������
�������:��1�����������ε��ڽǺͶ�����ʾ����AOD����BOC���ٸ��ݶԶ�����ȿɵ���AOD=��BOC��Ȼ���������ɵý⣻
��2�����ݡ�8���Ρ��Ľṹ�ص㣬���ݽ���д����8���Ρ��������Σ�Ȼ��ȷ�����ɣ�
��3�����ݣ�1���Ĺ�ϵʽ�����OCB����OAD���ٸ��ݽ�ƽ���ߵĶ��������DAM����PCM��Ȼ�����á�8���Ρ��Ĺ�ϵʽ��ʽ�������ɵý⣻
��4�����ݡ�8���Ρ�����B����D��ʾ����OCB����OAD��������D����P��ʾ����DAM����PCM��Ȼ����ݽ�ƽ���ߵĶ���ɵ���DAM����PCM=![]() ����OCB����OAD����Ȼ���������ɵ�֤��
����OCB����OAD����Ȼ���������ɵ�֤��
�⣺��1������AOD�У���AOD=180������A����D��
����BOC����BOC=180������B����C��
�ߡ�AOD=��BOC���Զ�����ȣ���
��180������A����D=180������B����C��
���A+��D=��B+��C��
��2�������е�M��O��N��
��M������1������AMD����CMP��
��O������4������AOD����COB����AOM����CON����AOM����COB����CON����AOD��
��N������1������ANP����CNB��
���ԣ���8���Ρ�ͼ�ι���6����
��3���ߡ�D=40������B=36����
���OAD+40��=��OCB+36����
���OCB����OAD=4����
��AP��CP�ֱ�����DAB����BCD�Ľ�ƽ���ߣ�
���DAM=![]() ��OAD����PCM=
��OAD����PCM=![]() ��OCB��
��OCB��
���ߡ�DAM+��D=��PCM+��P��
���P=��DAM+��D����PCM=![]() ����OAD����OCB��+��D=
����OAD����OCB��+��D=![]() ������4�㣩+40��=38�㣻
������4�㣩+40��=38�㣻
��4�����ݡ�8���Ρ�������ϵ����OAD+��D=��OCB+��B����DAM+��D=��PCM+��P��
���ԣ���OCB����OAD=��D����B����PCM����DAM=��D����P��
��AP��CP�ֱ�����DAB����BCD�Ľ�ƽ���ߣ�
���DAM=![]() ��OAD����PCM=
��OAD����PCM=![]() ��OCB��
��OCB��
��![]() ����D����B��=��D����P��
����D����B��=��D����P��
�����ã�2��P=��B+��D��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A. ��һ������ֻ��һ��ֱ������ֱ֪��ƽ��
B. ��ֱ�߱�������ֱ�����أ�ͬ���ڽǻ���
C. ���ཻ������ֱ�߽�ƽ����
D. �ڲ��ǵ�ƽ�����ഹֱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���������y=x2��4������ƽ��������λ��������ƽ��������λ���õ��������ߵĽ���ʽ�ǣ� ��
A. y=��x+2��2+2
B. y=��x��2��2��2
C. y=��x��2��2+2
D. y=��x+2��2��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�����Ϊ���������ǣ�������
A. 6��12��13 B. 3��4��7 C. 8��15��16 D. 5��12��13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1)3c3��2c2��8c��13c3��2c��2c2��3��
(2)8x2��4(2x2��3x��1)��
(3)5x2��2(3y2��5x2)��(��4y2��7xy)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ʱ�䣬С����СӨ��С���ʹ�յ�ѧУƹ�����Ҵ�ƹ����ʱֻ��һ��������������ֻ��ѡ���˴��һ����
��1�����ȷ��С�����һ�����ٴ��������������ѡȡһ�˴��һ������ǡ��ѡ�д�յĸ��ʣ�
��2�����ȷ��С�������У��á����ġ��ֱ����ķ��������������������˴��һ������Ϸ�����ǣ�����ͬʱ�조���ġ��ֱ����е�һ�����ƣ����ǡ�������������������ͬ����ô�������ϳ����������¿�ʼ����������������ġ����ֱ�����������ģ����û���״ͼ�ķ�����СӨ��С�����һ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��4�·�ij������������5������������ǩ�3������ô������²������¼�������£��ǣ� ��
A����2�� B��8�� C����8�� D��2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com