
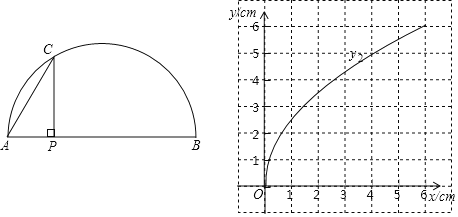
ЁОЬтФПЁПдкШчЭМЫљЪОЕФАыдВжаЃЌPЪЧжБОЖABЩЯвЛЖЏЕуЃЌЙ§ЕуPзїPCЁЭABгкЕуPЃЌНЛАыдВгкЕуCЃЌСЌНгACЃЎвбжЊAB=6cmЃЌЩшAЃЌPСНЕуМфЕФОрРыЮЊxcmЃЌPЃЌCСНЕуМфЕФОрРыЮЊy1cmЃЌAЃЌCСНЕуМфЕФОрРыЮЊy2cmЃЎ
аЁДЯИљОнбЇЯАКЏЪ§ЕФОбщЃЌЗжБ№ЖдКЏЪ§y1ЃЌy2ЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁДЯЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉАДееЯТБэжаздБфСПxЕФжЕНјааШЁЕуЁЂЛЭМЁЂВтСПЃЌЗжБ№ЕУЕНСЫy1ЃЌy2гыxЕФМИзщЖдгІжЕЃЛ
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.24 | 2.83 | 2.83 | 2.24 | 0 | |
y2/cm | 0 | 2.45 | 3.46 | 4.24 | 4.90 | 5.48 | 6 |
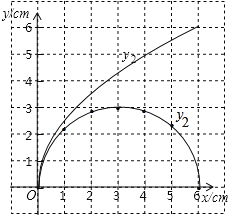
ЃЈ2ЃЉдкЭЌвЛЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіВЙШЋКѓЕФБэжаИїзщЪ§жЕЫљЖдгІЕФЕуЃЈxЃЌy1ЃЉЃЌЃЈxЃЌy2ЃЉЃЌВЂЛГіКЏЪ§y1ЃЌy2ЕФЭМЯѓЃЛ
ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБЁїAPCгавЛИіНЧЪЧ30ЁуЪБЃЌAPЕФГЄЖШдМЮЊ cmЃЎ
ЁОД№АИЁП(1)3;ЃЈ2ЃЉзїЭММћНтЮіЃЛЃЈ3ЃЉ4.5.
ЁОНтЮіЁП
ЃЈ1ЃЉвђЮЊPC=3ЪБЃЌPA=PB=3ЃЌЭЦГіPCЪЧЁбOЕФАыОЖМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉРћгУУшЕуЗЈЛГіКЏЪ§ЭМЯѓМДПЩЃЛ
ЃЈ3ЃЉРћгУЪ§аЮНсКЯЕФЫМЯыНтОіЮЪЬтМДПЩ.
ЃЈ1ЃЉвђЮЊPC=3ЪБЃЌPA=PB=3ЃЌ
ЁрPCЪЧЁбOЕФАыОЖЃЌ
ЁрPC=3cmЃЌМДx=3ЪБЃЌy1=3ЃЎ
ЃЈ2ЃЉРћгУУшЕуЗЈЛГіКЏЪ§ЭМЯѓМДПЩЃЎ
ЃЈ3ЃЉНсКЯЭМЯѓПЩжЊЃКЕБЁЯACP=30ЁуЪБЃЌAP=![]() AC=
AC=![]() ЁС
ЁС![]() AB=1.50cmЃЎ
AB=1.50cmЃЎ
ИљОнЖдГЦадЃЌНсКЯЭМЯѓПЩжЊЃКЕБЁЯCAP=30ЁуЪБЃЌPB=1.50cmЃЌPA=4.50cmЃЎ


 УћХЦжабЇПЮЪБзївЕЯЕСаД№АИ
УћХЦжабЇПЮЪБзївЕЯЕСаД№АИ УїЬьНЬг§ПЮЪБЬибЕЯЕСаД№АИ
УїЬьНЬг§ПЮЪБЬибЕЯЕСаД№АИ еуНаТПЮГЬШ§ЮЌФПБъВтЦРПЮЪБЬибЕЯЕСаД№АИ
еуНаТПЮГЬШ§ЮЌФПБъВтЦРПЮЪБЬибЕЯЕСаД№АИ жмжмЧхМьВтЯЕСаД№АИ
жмжмЧхМьВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФЯ.ББСНИідАСжГЁШЅФъЙВгадБЙЄ500ШЫЃЌЦфжаФЯдАСжГЁдБЙЄЪ§БШББдАСжГЁдБЙЄЪ§ЕФ2БЖЩй100ШЫ.
ЃЈ1ЃЉЧѓШЅФъФЯ.ББСНИідАСжГЁЕФдБЙЄЪ§ЃЛ
ЃЈ2ЃЉОКЫЫуЃЌШЅФъФЯдАСжГЁФъВњжЕБШББдАСжГЁФъВњжЕЩйm%.ББдАСжГЁШЫОљВњжЕБШФЯдАСжГЁШЫОљВњжЕЖр4m%ЃЌЧвСНИідАСжГЁШЫОљВњжЕВЛЕЭгкББдАСжГЁШЫОљВњжЕЕФ![]() .ЧѓmЕФжЕ.
.ЧѓmЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌCDЪЧЯвЃЌABЁЭCDЃЌДЙзуЮЊEЃЌЕуPдкЁбOЩЯЃЌСЌНгBPЁЂPDЁЂBCЃЎШєCD=![]() ЃЌsinP=
ЃЌsinP=![]() ЃЌдђЁбOЕФжБОЖЮЊЃЈЁЁЁЁЃЉ
ЃЌдђЁбOЕФжБОЖЮЊЃЈЁЁЁЁЃЉ

A. 8 B. 6 C. 5 D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
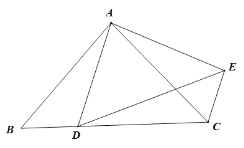
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=AC,DЪЧBCЩЯШЮвЛЕуЃЌAD=AEЧвЁЯBAC=ЁЯDAE.
ЃЈ1ЃЉШєEDЦНЗжЁЯAEC,ЧѓжЄЃКCEЁЮADЃЛ
ЃЈ2ЃЉШєЁЯBAC=90ЁуЃЌЧвDдкBCжаЕуЪБЃЌЪдХаЖЯЫФБпаЮADCEЕФаЮзДЃЌВЂЫЕУїФуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИпЫйЙЋТЗФГЪеЗбеОГіГЧЗНЯђгаБрКХЮЊ![]() ЕФЮхИіаЁПЭГЕЪеЗбГіПкЃЌМйЖЈИїЪеЗбГіПкУП20ЗжжгЭЈЙ§аЁПЭГЕЕФЪ§СПЗжБ№ЖМЪЧВЛБфЕФ.ЭЌЪБПЊЗХЦфжаЕФФГСНИіЪеЗбГіПкЃЌетСНИіГіПк20ЗжжгвЛЙВЭЈЙ§ЕФаЁПЭГЕЪ§СПМЧТМШчЯТЃК
ЕФЮхИіаЁПЭГЕЪеЗбГіПкЃЌМйЖЈИїЪеЗбГіПкУП20ЗжжгЭЈЙ§аЁПЭГЕЕФЪ§СПЗжБ№ЖМЪЧВЛБфЕФ.ЭЌЪБПЊЗХЦфжаЕФФГСНИіЪеЗбГіПкЃЌетСНИіГіПк20ЗжжгвЛЙВЭЈЙ§ЕФаЁПЭГЕЪ§СПМЧТМШчЯТЃК
ЪеЗбГіПкБрКХ |
|
|
|
|
|
ЭЈЙ§аЁПЭГЕЪ§СПЃЈСОЃЉ | 260 | 330 | 300 | 360 | 240 |
дк![]() ЮхИіЪеЗбГіПкжаЃЌУП20ЗжжгЭЈЙ§аЁПЭГЕЪ§СПзюЖрЕФвЛИіГіПкЕФБрКХЪЧ___________.
ЮхИіЪеЗбГіПкжаЃЌУП20ЗжжгЭЈЙ§аЁПЭГЕЪ§СПзюЖрЕФвЛИіГіПкЕФБрКХЪЧ___________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
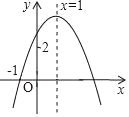
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+cЕФЖдГЦжсЪЧжБЯпxЃН1ЃЌЧвОЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌдђЯТСаНсТлЃКЂйabcЃМ0ЃЛЂк2aЉbЃН0ЃЛЂлaЃМЉ![]() ЃЛЂмШєЗНГЬax2+bx+cЉ2ЃН0ЕФСНИіИљЮЊx1КЭx2ЃЌдђЃЈx1+1ЃЉЃЈx2Љ3ЃЉЃМ0ЃЌе§ШЗЕФгаЃЈЁЁЁЁЃЉИіЃЎ
ЃЛЂмШєЗНГЬax2+bx+cЉ2ЃН0ЕФСНИіИљЮЊx1КЭx2ЃЌдђЃЈx1+1ЃЉЃЈx2Љ3ЃЉЃМ0ЃЌе§ШЗЕФгаЃЈЁЁЁЁЃЉИіЃЎ
A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
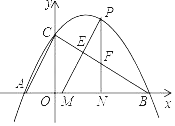
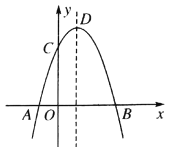
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+![]() ЕФЭМЯѓОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгыyжсЯрНЛгкЕуCЃЎЕуPЮЊЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPЗжБ№зіBCКЭxжсЕФДЙЯпЃЌНЛBCгкЕуEКЭFЃЌНЛxжсгкЕуMКЭNЃЎ
ЕФЭМЯѓОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгыyжсЯрНЛгкЕуCЃЎЕуPЮЊЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPЗжБ№зіBCКЭxжсЕФДЙЯпЃЌНЛBCгкЕуEКЭFЃЌНЛxжсгкЕуMКЭNЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЯпЖЮPEзюДѓжЕЃЌВЂЧѓГіЯпЖЮPEзюДѓЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШєSЁїPMNЃН3SЁїPEFЪБЃЌЧѓГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЮЊзјБъдЕуЃЌжБЯп
ЮЊзјБъдЕуЃЌжБЯп![]() ЗжБ№НЛ
ЗжБ№НЛ![]() жсИКАыжсКЭ
жсИКАыжсКЭ![]() жсе§Аыжсгк
жсе§Аыжсгк![]() СНЕуЃЌНЋ
СНЕуЃЌНЋ![]() би
би![]() жсЗелжС
жсЗелжС![]() ЃЌЧв
ЃЌЧв![]() ЕФУцЛ§ЮЊ8.
ЕФУцЛ§ЮЊ8.
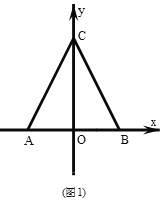
(1)ШчЭМЃЌЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
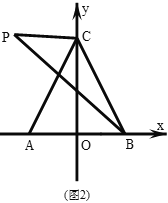
(2)ШчЭМЃЌЕу![]() ЮЊЕкЖўЯѓЯоФк
ЮЊЕкЖўЯѓЯоФк![]() ЩЯЗНЕФвЛЕуЃЌСЌНг
ЩЯЗНЕФвЛЕуЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪН(гУКЌ
ЕФКЏЪ§ЙиЯЕЪН(гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЛ
ЕФДњЪ§ЪНБэЪО)ЃЛ
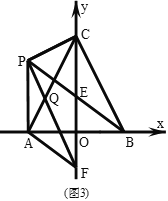
(3)ШчЭМЃЌдк(2)ЕФЬѕМўЯТЃЌСЌНг![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() жсИКАыжсЩЯвЛЕуЃЌ
жсИКАыжсЩЯвЛЕуЃЌ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() зјБъ.
зјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() КЭ
КЭ![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌХзЮяЯпЕФЖЅЕуЮЊ
ЃЌХзЮяЯпЕФЖЅЕуЮЊ![]() ЃЌЯТСаЫФИіХаЖЯЃКЂйЕБ
ЃЌЯТСаЫФИіХаЖЯЃКЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЂкШє
ЃЛЂкШє![]() ЃЌдђ
ЃЌдђ![]() ЃЛЂлХзЮяЯпЩЯгаСНЕу
ЃЛЂлХзЮяЯпЩЯгаСНЕу![]() КЭ
КЭ![]() ЃЌШє
ЃЌШє![]() ЃЌЧв
ЃЌЧв![]() ЃЌдђ
ЃЌдђ![]() ЃЛЂмЕу
ЃЛЂмЕу![]() ЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуЮЊ
ЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЁЂ
ЁЂ![]() ЗжБ№дк
ЗжБ№дк![]() жсКЭ
жсКЭ![]() жсЩЯЃЌЕБ
жсЩЯЃЌЕБ![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() жмГЄЕФзюаЁжЕЮЊ
жмГЄЕФзюаЁжЕЮЊ![]() .ЦфжаЃЌХаЖЯе§ШЗЕФађКХЪЧЃЈ ЃЉ
.ЦфжаЃЌХаЖЯе§ШЗЕФађКХЪЧЃЈ ЃЉ
A. ЂйЂкB. ЂкЂлC.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com