练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．解方程：
    （1）$\frac{0.1-0.2x}{0.3}$-1=$\frac{0.7-x}{0.4}$
    （2）3x-7（x-1）=3+2（x+3）

    分析 （1）方程整理后，去分母，去括号，移项合并，把x系数化为1，即可求出解；
    （2）方程去括号，移项合并，把x系数化为1，即可求出解．

    解答 解：（1）方程整理得：$\frac{1-2x}{3}$-1=$\frac{7-10x}{4}$，
    去分母得：4-8x-12=21-30x，
    移项合并得：22x=29，
    解得：x=$\frac{29}{22}$；
    （2）去括号得：3x-7x+7=3+2x+6，
    移项合并得：6x=-2，
    解得：x=-$\frac{1}{3}$．

    点评 此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．如图，在⊙O上有顶点C和动点P，位于直径AB的两侧，过点C作CP的垂线与PB的延长线交于点Q．已知⊙O的直径为10，tan∠ABC=$\frac{4}{3}$，则CQ最大值为（　　）
    A．5B．$\frac{15}{2}$C．$\frac{25}{4}$D．$\frac{20}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．在△ABC中，∠C=90°，AB的垂直平分线DE交AB于E，交BC于D，且CD：BD=1：2，BC=6cm，则D到AB的距离为多少（　　）
    A．1.5cmB．2cmC．3cmD．4cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如果10b=n，那么称b为n的劳格数，记为b=d （n），由定义可知：10b=n与b=d （n）所表示的是b、n两个量之间的同一关系．
    （1）根据劳格数的定义，填空：d（10）=1，d（10-2）=-2；
    劳格数有如下运算性质：
    若m、n为正数，则d（mn）=d（m）+d（n），d（$\frac{m}{n}$）=d（m）-d（n）．
    根据运算性质，填空：$\frac{d（{a}^{3}）}{d（a）}$=3（a为正数）．
    （2）下表中与数x对应的劳格数d （x）有且只有两个是错误的，请找出错误的劳格数，说明理由并改正．
    x1.5356891227
    d（x）3a-b+c2a-ba+c1+a-b-c3-3a-3c4a-2b3-b-2c6a-3b

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列调查适合作抽样调查的是（　　）
    A．了解巫溪网“今日巫溪”栏目的阅览率
    B．了解某甲型H1N1确诊病人同机乘客的健康状况
    C．了解某班每个学生家庭电脑的数量
    D．对“歼20”隐形战斗机零部件的检查

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，在Rt△ABC中，∠ACB=90°，I为Rt△ABC的内心，过点I作ID∥BC，交斜边AB于点D，连接CI，则∠CID=135°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．用配方法解方程x2+4x-5=0，下列配方正确的是（　　）
    A．（x+2）2=1B．（x+2）2=5C．（x+2）2=9D．（x+4）2=9

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．已知：如图，在?ABCD中，延长AB到点E，使BE=AB，连接DE交BC于点F．求证：△BEF≌△CDF．

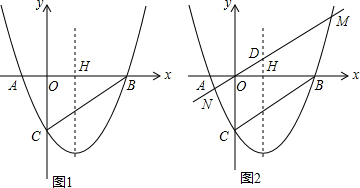
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，已知抛物线y=x2+bx+c交x轴于点A（-1，0）、B（2，0），交y轴于点C，抛物线的对称轴交x轴于点H，直线y=kx（k＞0）交抛物线于点M、N（点M在N的右侧），交抛物线的对称轴于点D．
    （1）求b和c的值；
    （2）如图（1），若将抛物线y=x2+bx+c沿y轴方向向上平移$\frac{5}{4}$个单位，求证：所得新抛物线图象均在直线BC的上方；
    （3）如图（2），若MN∥BC．
    ①连接CD、BM，判断四边形CDMB是否为平行四边形，说明理由；
    ②以点D为圆心，DH长为半径画圆⊙D，点P、Q分别为抛物线和⊙D上的点，试求线段PQ长的最小值．

    查看答案和解析>>

    同步练习册答案