
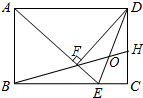
 矩形ABCD中,AD=$\sqrt{2}$AB,AE平分∠BAD,DF⊥AE于F,BF交DE、CD于O、H,下列结论:①∠DEA=3∠EDC;②BF=FH;③OE=OD;④BC-CH=2EF,其中结论正确的个数有( )
矩形ABCD中,AD=$\sqrt{2}$AB,AE平分∠BAD,DF⊥AE于F,BF交DE、CD于O、H,下列结论:①∠DEA=3∠EDC;②BF=FH;③OE=OD;④BC-CH=2EF,其中结论正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由AE为直角的平分线,得到∠BAE=∠DAE=45°,可得出三角形ABE和三角形AFD为等腰直角三角形,利用勾股定理得到AE=$\sqrt{2}$AB,由已知AD=$\sqrt{2}$AB,得到AD=AE,即三角形ADE为等腰三角形,求出底角∠AED度数为67.5°,由平角的定义及∠AEB与∠AED度数求出∠DEC为67.5°,等量代换得到∠DEA=∠DEC,选项①正确;过F作FG垂直于AD,利用三线合一得到G为AD中点,利用平行线等分线段定理得到F为BH中点,即BF=FH,选项②正确;由AD=$\sqrt{2}$AF=$\sqrt{2}$AB,得到AF=AB,即三角形ABF为等腰三角形求出底角∠AFB=67.5°,利用对顶角相等得到∠EFH为67.5°,进而求出∠DFO为22.5°,根据一对直角相等,∠DEA=∠DEC=67.5°,确定出∠EDF=∠EDC=22.5°,确定出∠OFD=∠ODF=22.5°,等角对等边得到OD=OF,由∠OFE=∠OEF=67.5°,等角对等边得到OF=OE,等量代换得到OE=OD,选项③正确;同理得到M为BC中点,即FM为三角形BHC的中位线,得到CH=2FM,三角形EFM为等腰直角三角形,由等腰三角形的性质可知FM=ME,可得出BC-CH=2CM-2FM=2CM-2ME=2EF,选项④正确.
解答 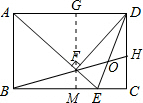 解:∵四边形ABCD为矩形,AE平分∠BAD,
解:∵四边形ABCD为矩形,AE平分∠BAD,
∴∠BAE=∠DAE=∠AEB=45°,
∵∠AFD=∠ABE=90°,
∴△AFD与△ABE都为等腰直角三角形,即AF=DF,AB=BE,
∴AE=$\sqrt{2}$AB,
又∵AD=$\sqrt{2}$AB,
∴AD=AE,
∴∠AED=∠ADE=67.5°,
∴∠DEC=180°-45°-67.5°=67.5°,
∴∠DEA=∠DEC,选项①正确;
过F作GM⊥AD,与AD交于G点,与BC交于M点,
利用三线合一得到G为AD中点,
∴F为BH中点,M为BC中点,
∴BF=FH,选项②正确;
∵AD=$\sqrt{2}$AF,AD=$\sqrt{2}$AB,
∴AF=AB,
∴∠AFB=67.5°,
∴∠OFE=∠OEF=67.5°,
∴OE=OF,
∴∠ODF=∠OFD=22.5°,
∴OF=OD,
∴OD=OE,选项③正确;
∴∠DEF=67.5°-45°=22.5°,∠EDC=90°-67.5°=22.5°,
∴∠EDF=∠DEC,
∵EF⊥DF,EC⊥CD,
∴EF=EC,
∵△EFM为等腰直角三角形,
∴FM=ME,
∴BC-CH=2CM-2FM=2CM-2ME=2EF,选项④正确,
则正确的序号有4个.
故选:D
点评 此题考查了四边形综合题,涉及的知识有:矩形的性质,等腰三角形的判定与性质,等腰直角三角形的判定与性质,中位线定理,平行线等分线段定理,角平分线定理,利用了等量代换的思想,熟练掌握判定与性质是解本题的关键.


科目:初中数学 来源: 题型:选择题
| 分数(分) | 60 | 70 | 80 | 90 | 100 |
| 人数(人) | 1 | 1 | 5 | 2 | 1 |
| A. | 学生成绩的极差是4 | B. | 学生成绩的众数是1 | ||
| C. | 学生成绩的中位数是80 | D. | 学生成绩的平均数是80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
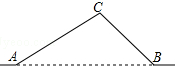 如图,从A地到B地的公路需经过C地,图中AC=20千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=20千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
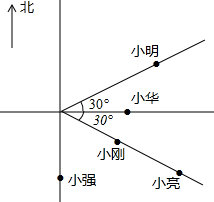 小李、小明、小刚、小强、小华、小亮是很要好的伙伴,他们家的位置如图所示.一天,小李说:“如果以我家为中心,你们各自家的位置在哪儿知道吗?”其余小伙伴说到:“当然知道了.”小李说:“这样吧,你们若回答出下列问题,就证明你们知道.”
小李、小明、小刚、小强、小华、小亮是很要好的伙伴,他们家的位置如图所示.一天,小李说:“如果以我家为中心,你们各自家的位置在哪儿知道吗?”其余小伙伴说到:“当然知道了.”小李说:“这样吧,你们若回答出下列问题,就证明你们知道.”查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
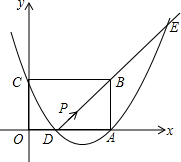 如图,已知矩形OABC,点A,C分别在x,y轴上,抛物线y=ax2+bx+c经过A(12,0),D(6,0)两点,且与y轴交于点C(0,8).动点P从点D出发,以每秒1个单位的速度沿射线DB方向运动,设P运动的时间为t(秒),射线DB交抛物线于E.
如图,已知矩形OABC,点A,C分别在x,y轴上,抛物线y=ax2+bx+c经过A(12,0),D(6,0)两点,且与y轴交于点C(0,8).动点P从点D出发,以每秒1个单位的速度沿射线DB方向运动,设P运动的时间为t(秒),射线DB交抛物线于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com