
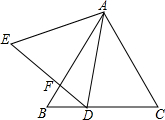
 如图,正△ABC的边长为6,点D是BC边上一点,连结AD,将AD绕点A顺时针旋转60°得AE,连结DE交AB于点F.
如图,正△ABC的边长为6,点D是BC边上一点,连结AD,将AD绕点A顺时针旋转60°得AE,连结DE交AB于点F.分析 (1)先证△AED是等边三角形,从而∠BDF=∠EAF;
(2)证明△BDF∽△CAD,列出相似比例关系即可;
(3)过点D作DG⊥AC于G,求出DG、AG,就可求出AD,而AD=AE.
解答 解:(1)∵AE=AD,∠DAE=60°,
∴△AED是等边三角形,
∴∠AED=∠ADE=60°,
∵∠ABC=60°,
∴∠BDF=∠EAF,
∵∠BAD=20°,
∴∠EAF=40°,
∴∠BDF=40°;
(2)∵∠EDA=60°,
∴∠BDF+∠ADC=120°,
∵∠ACB=60°,
∴∠ADC+∠DAC=120°,
∴∠BDF=∠DAC,
∴△BDF∽△CAD,
∴$\frac{BF}{BD}=\frac{CD}{AC}$,
∵BF=y,BD=x,AB=BC=AC=6,
∴$\frac{y}{x}=\frac{6-x}{6}$,
∴$y=-\frac{1}{6}{x}^{2}+x$;
(3)过点D作DG⊥AC于G,如图,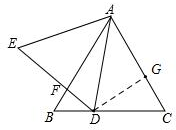
∵BC=6,$\frac{BD}{CD}=\frac{1}{2}$,
∴BD=2,CD=4,
∵∠ACB=60°,
∴CG=2,DG=2$\sqrt{3}$,
∴AG=4,
∴AD=$2\sqrt{7}$,
∵△AED是等边三角形,
∴AE=AD=$2\sqrt{7}$.
点评 本题考查了等边三角形的性质、旋转的性质、三角形内角和定理、相似三角形的判定与性质、特殊角的三角函数、勾股定理等知识点,难度中等.第(1)问的关键是转移角度;知道“一线三等角相似模型”是迅速解决第(2)问的关键;对于线段长度的求法,往往构造直角三角形,利用勾股定理解决.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
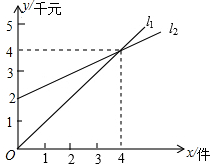 如图,l1、l2分别表示某种产品的销售收入与销售件数的函数关系图象和销售成本与件数的函数关系图象.
如图,l1、l2分别表示某种产品的销售收入与销售件数的函数关系图象和销售成本与件数的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-3)2+2 | B. | y=x2+5 | C. | y=(x+3)2+2 | D. | y=x2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x+1=5x+7 | B. | $\frac{1}{{x}^{2}}$+x-1=0 | ||
| C. | x2-5=0 | D. | ax2-bx=5(a和b为常数) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com