
【题目】如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F.

(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD;
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
试题(1)根据矩形的性质和折叠的性质可得:AB=DC=DE,∠BAD=∠BCD=∠BED=90°,根据AAS可证△ABF≌△EDF,根据全等三角形的性质可证BF=DF;
(2)根据全等三角形的性质可证:FA=FE,根据等边对等角可得:∠FAE=∠FEA,根据三角形内角和定理可证:2∠AEF +∠AFE =2∠FBD+∠BFD =180°,所以可证∠AEF=∠FBD,根据内错角相等,两直线平行可证AE∥BD;
(3)根据矩形的性质可证:AD=BC=BE,AB=CD=DE,BD=DB,根据SSS可证:△ABD≌△EDB,根据全等三角形的性质可证:∠ABD=∠EDB,根据等角对等边可证:GB=GD,根据HL可证:△AFG≌△EFG,根据全等三角形的性质可证:∠AGF=∠EGF,所以GH垂直平分BD.
试题解析:(1)∵长方形ABCD,
∴AB=DC=DE,∠BAD=∠BCD=∠BED=90°,
在△ABF和△DEF中,
∴△ABF≌△EDF(AAS),
∴BF=DF.
(2)∵△ABF≌△EDF,
∴FA=FE,
∴∠FAE=∠FEA,
又∵∠AFE=∠BFD,且2∠AEF +∠AFE =2∠FBD+∠BFD =180°,
∴∠AEF=∠FBD,
∴AE∥BD,
(3)∵长方形ABCD,
∴AD=BC=BE,AB=CD=DE,BD=DB,
∴△ABD≌△EDB(SSS),
∴∠ABD=∠EDB,
∴GB=GD,
在△AFG和△EFG中,
∠GAF=∠GEF=90°,
FA=FE,
FG=FG,
∴△AFG≌△EFG(HL),
∴∠AGF=∠EGF,
∴GH垂直平分BD.
【方法II】
(1)∵△BCD≌△BED,
∴∠DBC=∠EBD
又∵长方形ABCD,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠EBD=∠ADB,
∴FB=FD.
(2)∵长方形ABCD,
∴AD=BC=BE,
又∵FB=FD,
∴FA=FE,
∴∠FAE=∠FEA,
又∵∠AFE=∠BFD,且2∠AEF +∠AFE =2∠FBD+∠BFD =180°,
∴∠AEF=∠FBD,
∴AE∥BD,
(3)∵长方形ABCD,
∴AD=BC=BE,AB=CD=DE,BD=DB,
∴△ABD≌△EDB,
∴∠ABD=∠EDB,
∴GB=GD,
又∵FB=FD,
∴GF是BD的垂直平分线,
即GH垂直平分BD.


科目:初中数学 来源: 题型:
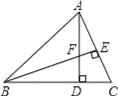
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
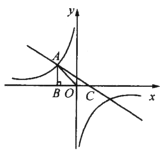
【题目】如图,已知反比例函数![]() (k<0)的图像经过点A(
(k<0)的图像经过点A(![]() ,m),过点A作AB⊥x轴于点,且△AOB的面积为
,m),过点A作AB⊥x轴于点,且△AOB的面积为![]() .
.
(1)求k和m的值;
(2)若一次函数y=ax+1的图像经过点A,并且与x轴相交于点C,求∠ACO的度数及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠C,AD⊥BE于点F,BC⊥BE,点E,D,C在同一条直线上.
(1)判断AB与CD的位置关系,并说明理由;
(2)若∠ABC=120°,求∠BEC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用相同的小正方形按照某种规律进行摆放.根据图中小正方形的排列规律,猜想第![]() 个图中小正方形的个数为___________(用含
个图中小正方形的个数为___________(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,
,![]() .
.
(1)求反比例函数的解析式:
(2)若点![]() 为
为![]() 轴上一动点,当
轴上一动点,当![]() 是等腰三角形时,直接写出点
是等腰三角形时,直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区活动中心为中老年舞蹈队统一队服和道具,准备购买 10 套某种品牌的舞蹈鞋,每双舞蹈鞋配 x(x≥2)个舞蹈扇,供舞蹈队队员使用.该社区附近 A,B 两家超市都有这种品牌的舞蹈鞋和舞蹈扇出售,且每双舞蹈鞋的标价均为 30 元,每个舞蹈扇的标价为 3 元,目前两家超市同时在做促销活动:
A 超市:所有商品均打九折(按标价的 90%)销售;
B 超市:买一双舞蹈鞋送 2 个舞蹈扇.
设在 A 超市购买舞蹈鞋和舞蹈扇的费用为![]() (元),在 B 超市购买舞蹈鞋和舞蹈扇的费用为
(元),在 B 超市购买舞蹈鞋和舞蹈扇的费用为 ![]() (元).请解答下列问题:
(元).请解答下列问题:
(1)分别写出 ![]() ,
,![]() 与 x 之间的关系式;
与 x 之间的关系式;
(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com