
分析 (1)根据抛物线的顶点坐标可设出其顶点式,再由抛物线过A(1,0),可得出抛物线的解析式,再把A点坐标代入直线y2=x+m求出m的值即可;
(2)在同一坐标系内画出一次函数与二次函数的图象,利用函数图象即可得出结论;
(3)根据(2)中函数图象可直接得出结论.
解答 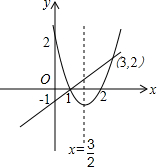 解:(1)∵抛物线y1=ax2+bx+c的顶点坐标为($\frac{3}{2},-\frac{1}{4}$),
解:(1)∵抛物线y1=ax2+bx+c的顶点坐标为($\frac{3}{2},-\frac{1}{4}$),
∴y1=a(x-$\frac{3}{2}$)2-$\frac{1}{4}$,
∵抛物线经过点A(1,0),
∴a(1-$\frac{3}{2}$)2-$\frac{1}{4}$=1,解得a=1,
∴y1=(x-$\frac{3}{2}$)2-$\frac{1}{4}$.
∵直线y2=x+m恰好也经过点A,
∴1+m=0,解得m=-1,
∴y2=x-1;
(2)如图所示,当1<x<3时,y2>y1;
(3)由图可知,当0≤x≤2时y1的最小值为-$\frac{1}{4}$,y2的最小值为-1.
点评 本题考查的是二次函数与不等式组,根据题意画出函数图象,利用数形结合求解是解答此题的关键.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一个由多个相同小正方体堆积而成的几何体从上面看到的形状图,图中所示数字为该位置小正方形的个数,请你画出它从正面和从左面看到的形状图.
如图是一个由多个相同小正方体堆积而成的几何体从上面看到的形状图,图中所示数字为该位置小正方形的个数,请你画出它从正面和从左面看到的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
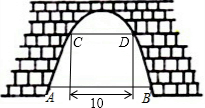 如图是一座抛物线拱形桥,在正常水位时,水面AB宽是20m,水位上升3m就达到警戒线CD,这是水面宽度为10m,请构建适当的水平直角坐标系求抛物线所对应的函数表达式,并求水位到达警戒线时拱顶与水面之间的距离.
如图是一座抛物线拱形桥,在正常水位时,水面AB宽是20m,水位上升3m就达到警戒线CD,这是水面宽度为10m,请构建适当的水平直角坐标系求抛物线所对应的函数表达式,并求水位到达警戒线时拱顶与水面之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com