
����Ŀ����ͼ��ֱ������ϵ�У�ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ����A��B���㣬��֪A�����������2.
��ͼ����A��B���㣬��֪A�����������2.
��1�����������Ľ���ʽ.
��2����ֱ��![]() ��x������ƽ��6����λ���뷴���������ڵڶ������ڽ��ڵ�C.����P��y�����������˶������߶�PA���߶�PC֮��ﵽ���ʱ�����P������.
��x������ƽ��6����λ���뷴���������ڵڶ������ڽ��ڵ�C.����P��y�����������˶������߶�PA���߶�PC֮��ﵽ���ʱ�����P������.

���𰸡���1��![]() ����2��P��0,6��
����2��P��0,6��
�������������������1������õ�A�����꣬�����ô���ϵ������÷����������Ľ���ʽ���ɣ���2������AC����������������֮��С�ڵ�����֪����A��C��P������ʱ��PA-PC<AC����A��C��P������ʱ��PA-PC=AC����ˣ�����P��ֱ��AC��y��Ľ���ʱ��PA-PCȡ�����ֵ.�����ƽ�ƺ�ֱ�ߵĽ���ʽ�������ƽ�ƺ�ֱ���뷴����������ͼ��Ľ������꣬�����ֱ��AC�Ľ���ʽ��������õ�P������.
���������
![]() ��һ�κ���
��һ�κ���![]() ��
��![]() ����
����![]() ��
��
��ã�![]() ������A������Ϊ��-4��2����
������A��������-4��2����
����A��-4��2���ڷ���������![]() ��ͼ���ϣ�
��ͼ���ϣ�
��k=-4��2=-8��
�෴���������ı���ʽΪ![]() ��
��
![]() ����AC����������������֮��С�ڵ�����֪����A��C��P������ʱ��PA-PC<AC����A��C��P������ʱ��PA-PC=AC����ˣ�����P��ֱ��AC��y��Ľ���ʱ��PA-PCȡ�����ֵ.
����AC����������������֮��С�ڵ�����֪����A��C��P������ʱ��PA-PC<AC����A��C��P������ʱ��PA-PC=AC����ˣ�����P��ֱ��AC��y��Ľ���ʱ��PA-PCȡ�����ֵ.
��ƽ�ƺ�ֱ����x�ύ�ڵ�F����F��6��0��
��ƽ�ƺ��ֱ�߽���ʽΪ![]() ��
��
��F��6��0������![]() �ã�b=3
�ã�b=3
��ֱ��CF����ʽ��![]()
��![]() 3=
3=![]() ����ã�
����ã�![]() ��
��
��C��-2��4��
��A��C��������ֱ�ΪA��-4��2����C��-2��4��
��ֱ��AC�ı���ʽΪ![]() ��
��
��ʱ��P������ΪP��0��6��.
�㾦��������һ�κ����뷴�����������ۺ��⣬��Ҫ�������ô���ϵ���������Ľ���ʽ��һ�κ����뷴���������Ľ������꣬��������һ�κ����������������������ǽ���Ĺؼ�.
�����͡������
��������
26
����Ŀ�����ı���ABCD�ı�AB��ADΪ�ױ߷ֱ�������������ABF��ADE,����EB.
(1)���ı���ABCDΪ������ʱ(��ͼ1),�Ա�AB��ADΪб�߷ֱ������������ֱ��������ABF��ADE������EB��FD���߶�EB��FD��������ϵ�� .
(2)���ı���ABCDΪ����ʱ(��ͼ2),�Ա�AB��ADΪб�߷ֱ����ڲ�������ֱ��������ABF��ADE������EF��BD���߶�EF��BD����������������ϵ?�����֤��;
(3)���ı���ABCDΪƽ���ı���ʱ(��ͼ3),�Ա�AB��ADΪб�߷ֱ���ƽ���ı����ڲ⡢���������ֱ��������ABF��ADE������EAD����FBA�Ķ��Ƕ�Ϊ��������EF��BD������ΪG����������ʾ����EGD����˵������.
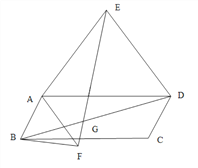
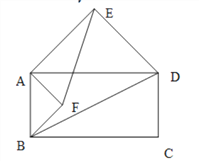

ͼ1 ͼ2 ͼ3
���𰸡���1��EF=BD����2��EF=![]() BD����3��
BD����3��![]()
����������������1�������ε����ʡ��ȱ������ε����ʺ�ȫ�������ε�֤��������֤����AFD�ա�ABE����ȫ�������ε����ʼ��ɵõ�EB=FD����2�����ݵ���ֱ�������ε����ʿɵ�![]() ����֤�á�BAD=��FAE�������ж���BAD����FAE ���������������ε����ʿɵ�
����֤�á�BAD=��FAE�������ж���BAD����FAE ���������������ε����ʿɵ�![]() �����ɵ�
�����ɵ�![]() ����3��
����3��![]() ����֤��BFA����DEA�����ɵ�
����֤��BFA����DEA�����ɵ�![]() ��
��
��֤��![]() �����ԡ�BAD����FAE������ȫ�������ε����ʼ��ɵ�
�����ԡ�BAD����FAE������ȫ�������ε����ʼ��ɵ�![]() �����ɡ�AHE=��DHG�����ɵ�
�����ɡ�AHE=��DHG�����ɵ�![]() .
.
��⣺(1)EF=BD��
�������£�
�ı���ABCDΪ�����Σ�
��AB=AD��
�����ı���ABCD�ı�AB��ADΪ�߷ֱ���������ȱ�������ABF��ADE��
��AF=AE����FAB=��EAD=60����
�ߡ�FAD=��BAD+��FAB=90��+60��=150����
��BAE=��BAD+��EAD=90��+60��=150����
���FAD=��BAE��
�ڡ�AFD�͡�ABE�У� 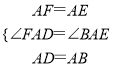 ��
��
���AFD�ա�ABE��
��EB=FD��
(2)EF=![]() BD.
BD.
֤�����ߡ�AFBΪ����ֱ��������
��![]() ,��FAB=45��
,��FAB=45��
ͬ���� ![]() ,��EAD=45�� ���BAD+��FAD=��EAD+��DAF
,��EAD=45�� ���BAD+��FAD=��EAD+��DAF
����BAD=��FAE
��![]() ��
�� ![]() ��
��![]()
���BAD����FAE ��![]()
���� ![]()
��3���⣺ ![]()
�ߡ�AFBΪ����ֱ������������FB=FA��
ͬ����ED=EA����![]() ��
��
�֡�![]() �����BFA����DEA��
�����BFA����DEA��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���BAD����FAE��
��![]() ��
��
�֡ߡ�AHE=��DHG��
��![]() .
.


 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����κ���y=ax2+bx+c��ͼ�����ϣ�ͼ���㣨��1��2���ͣ�1��0��������y�ύ�ڸ����ᣬ�����������ۣ���a��0����b��0����c��0����a+b+c=0����b2��4ac��0����2a��b��0��������ȷ���������_____��
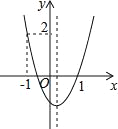
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
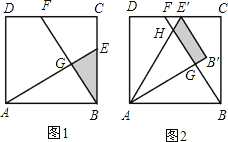
����Ŀ����֪����ͼ1�������Ϊ3��������ABCD�У�E��F�ֱ���BC��CD���ϵ����㣬AE��BF�ڵ�G����BE=1��
��1����֤����ABE�ա�BCF��
��2�������ABE����BCF�ص����֣�����BEG���������
��3���ֽ���ABE�Ƶ�A��ʱ�뷽����ת����AB��E������ͼ2����ʹ��E����CD���ϵĵ�E����������ABE����תǰ������BCF�ص����ֵ�����Ƿ����˱仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B��C�����������ϵ�λ����ͼ��ʾ�����DZ�ʾ�����ֱ���a��b��c
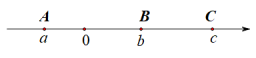
(1) ��գ�abc________0��a��b________ac��ab��ac________0������������������������������
(2) ��|a|��2���ҵ�B����A��C�ľ������
�� ��b2��16ʱ����c��ֵ
�� ��b��c֮���������ϵ
�� P��������B��C����֮���һ���������P��ʾ����Ϊx����P�����˶������У�bx��cx��|x��c|��10|x��a|��ֵ���ֲ��䣬��b��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
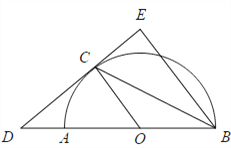
����Ŀ����ͼ����֪![]() ��
��![]() ��ֱ����CD��
��ֱ����CD��![]() ������C��
������C�� ![]() .
.
��1����֤��BC ��![]() ��ƽ����.
��ƽ����.
��2����DC=8�� ![]() �İ뾶OA=6����CE�ij�.
�İ뾶OA=6����CE�ij�.
���𰸡���1��֤������������2��4.8
����������������1����![]() ���Ƴ�
���Ƴ�![]() ����
����![]() ���Ƴ�
���Ƴ�![]() ���ɵ�
���ɵ�![]() .��2����
.��2����![]() �����OD����
�У����OD����![]() ���ɵ�
���ɵ�![]() ���ɴ˼��ɽ������.
���ɴ˼��ɽ������.
��⣺��1��֤������Ϊ![]() ��
��
����![]() ��
��
����Ϊ![]() ��
��
����![]() ��
��
�ʿɵ�![]() ��
��
���ɵ�![]() ��
��![]() ��ƽ����.
��ƽ����.
��2����ΪDE��![]() �����ߣ�
�����ߣ�
����![]() ������
������![]() ��DC=8��OC=OA=6,����
��DC=8��OC=OA=6,����![]() ��
��
����Ϊ![]() ��
��
����![]() ��
��
����![]() ��
��
���ɵ�EC=4.8
�㾦��������Ҫ���������ߵ����ʼ����������ε�Ӧ�ã���Ŀ�Ѷ����У����ۺ������������֪ʶ���ǽ���Ĺؼ�.
�����͡������
��������
23
����Ŀ����ʳƷ��ȫ���ܵ�ȫ���Ĺ㷺��ע��������ij��ѧ�Բ���ѧ����ʳƷ��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ�����������.
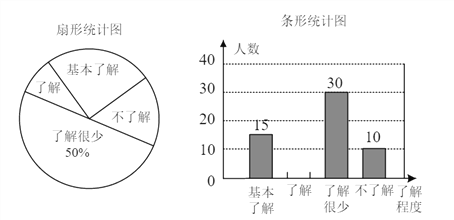
��1�������ʾ������ѧ������_____�ˣ�����ͳ��ͼ���������˽�����������Ӧ���ε�Բ�Ľ�Ϊ_____.
��2���벹ȫ����ͳ��ͼ.
��3��������ѧ����ѧ��900�ˣ���������������������Ƹ���ѧѧ���ж�ʳƷ��ȫ֪ʶ�ﵽ���˽������������˽����̶ȵ�������.
��4�����Ӷ�ʳƷ��ȫ֪ʶ�ﵽ���˽����̶ȵ�2��Ů����2�������������ȡ2�˲μ�ʳƷ��ȫ֪ʶ������������״ͼ���б������ǡ�ó鵽1��������1��Ů���ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧ����ѧҵ�������ػ�����Ӱ��ѧ���Դ�ѧϰ��̬�ȣ�Ϊ�����н������ŶԲ���ѧУ�İ��꼶ѧ���Դ�ѧϰ��̬�Ƚ�����һ�γ������飨��ѧϰ̬�ȷ�Ϊ�����㼶��A������ѧϰ�ܸ���Ȥ��B������ѧϰ�ϸ���Ȥ��C������ѧϰ������Ȥ�����������������Ƴ�ͼ����ͼ����ͳ��ͼ�����������������ͼ���ṩ����Ϣ������������⣺
��1���˴γ��������У��������� ��ѧ����
��2����ͼ������������
��3�����ͼ����C����ռ��Բ�ĽǵĶ�����
��4�����ݳ���������������������н�8000�����꼶ѧ���д�Լ�ж�����ѧ��ѧϰ̬�ȴ�꣨������A����B������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȥ�Ϸ�������Ҷ����ij��A�����г���ÿ��mԪ�ļ۸����40����Ҷ���ֵ�B�����г�ʱ����ͬ���IJ�Ҷ��A�����г�Ҫ���ˣ�ÿ���ļ۸��ΪnԪ�����������B�����г�����60��ͬ���IJ�Ҷ�����������ʱ��ÿ��![]() Ԫ�ļ۸�ȫ������������Ҷ����ô�ڲ������������ص�������������������������
Ԫ�ļ۸�ȫ������������Ҷ����ô�ڲ������������ص�������������������������
A.һ��ӯ��B.һ������
C.��ӯ����D.ӯ������ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
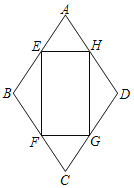
����Ŀ����ͼ������ABCD�У�AB=1����A=60����EFGH�Ǿ��Σ����εĶ��㶼�����εı��ϣ���AE=AH=x��0��x��1�������ε����ΪS��
��1����S����x�ĺ�������ʽ��
��2����EFGH��������ʱ����S��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶ѧ��С����Сǿ��С�쵽ij���вμ������ʵ������ڻ�����Dz�����ij��ˮ�������۹�������֪��ˮ���Ľ���Ϊ8Ԫ/ǧ�ˣ������������ڻ������ĶԻ���
С���������10Ԫ/ǧ�˵ļ۸����ۣ���ôÿ����۳�300ǧ�ˣ�
Сǿ�����ÿǧ�˵�����Ϊ3Ԫ����ôÿ����۳�250ǧ�ˣ�
С�죺�����13Ԫ/ǧ�˵ļ۸����ۣ���ôÿ��ɻ�ȡ����750Ԫ��
������=�����ۼ�-���ۣ�![]() ��������
��������
��1����������ǵĶԻ���д�±���
���۵���x��Ԫ/kg�� | 10 | 11 | 13 |
������y��kg�� |
��2��������ݱ����е���Ϣ�ж�ÿ���������y��ǧ�ˣ������۵���x��Ԫ��֮����������ĺ�����ϵ������y��ǧ�ˣ���x��Ԫ����x��0���ĺ�����ϵʽ��
��3����ó�����������ˮ��ÿ���ȡ������ΪWԪ����W��x�ĺ�����ϵʽ�������۵���Ϊ��ֵʱ��ÿ��ɻ�õ����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com