
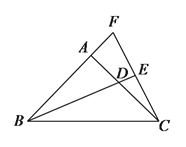
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的平分钱,
的平分钱,![]() 垂足是
垂足是![]() ,
,![]() 和
和![]() 的延长线交于点
的延长线交于点![]() .
.
(![]() )请找出与
)请找出与![]() 相等的所有的角,并证明其中一个.
相等的所有的角,并证明其中一个.
(![]() )求证:
)求证:![]() .
.
【答案】(![]() )
)![]() ,理由见解析;(2)证明见解析.
,理由见解析;(2)证明见解析.
【解析】试题分析:(1)与∠F相等的所有角为∠ADB、∠EDC、∠BCF,选择证明∠F=∠BCF,由已知条件不难证明△FBE≌△CBE,即可证明∠F=∠BCF;(2)先计算出∠ABC和∠ACB的度数,继而求出∠ABD的度数,再由等腰三角形中,已知顶角∠ABC的度数,求出底角∠FCB的度数,接着求出∠ACF的度数,得出∠ABD=∠FCA,再由AB=AC以及∠BAD=∠FAC可得△BAD≌△CAF,所以BD=CF,又因为CE=EF,得证.
试题解析:
(![]() )∠F=∠ADB=∠EDC=∠BCF,
)∠F=∠ADB=∠EDC=∠BCF,
证明∠F=∠BCF,
∵BD平分∠ABC,
∴∠FBE=∠CBE,
∵CE⊥BD于点E,
∴∠FEB=∠CEB=90°,
再△FBE和△CBE中,
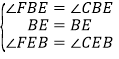 ,
,
∴△FBE≌△CBE(ASA),
∴∠F=∠BCF;
(![]() )∵在Rt△ABC中,∠BAC=90°,AB=AC,
)∵在Rt△ABC中,∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵BE平分∠ABC,
∴∠ABD=![]() ∠ABC=22.5°,
∠ABC=22.5°,
由(1)可知,∠F=∠FCB=![]() ×(180°-∠ABC)=67.5°,
×(180°-∠ABC)=67.5°,
∴∠FCA=∠FCB-∠ACB=67.5°-45°=22.5°,
∴∠ABD=∠FCA,
在△BAD和△CAF中,
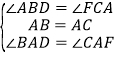 ,
,
∴△BAD≌△CAF(ASA),
∴BD=CF,
∵CE=EF,
∴BD=2EC.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC⊥AB,O为AC的中点,经过点O的直线交AD于E,交BC于F,连结AF、CE,现在添加一个适当的条件,使四边形AFCE是菱形,下列条件:①OE=OA;②EF⊥AC;③AF平分∠BAC;④E为AD中点.正确的有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是![]() ,每个小括的顶点叫做格点.
,每个小括的顶点叫做格点.
(![]() )如图
)如图![]() ,点
,点![]() ,
,![]() ,
,![]() 是小正方形的顶点,直接写出
是小正方形的顶点,直接写出![]() 的度数.
的度数.
(![]() )在图
)在图![]() 中以格点为顶点画一个面积为
中以格点为顶点画一个面积为![]() 的正方形.
的正方形.
(![]() )在图
)在图![]() 中以格点为顶点画一个三角形,使三角形三边长分别为
中以格点为顶点画一个三角形,使三角形三边长分别为![]() ,
,![]() ,
,![]() .
.
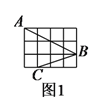

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),
当x1﹤x2时,都有y1﹤y2,称该函数为增函数.根据以上定义,可以判断下面所给的函数中,是增函数的有______________(填上所有正确答案的序号).
① y = 2x; ② y =![]() x+1; ③ y = x2 (x>0); ④
x+1; ③ y = x2 (x>0); ④ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线l1:y=2x+b与直线l2:y=mx+4相交于点P(1,3),利用图像:
(1)解关于x,y的二元一次方程组:![]()
(2)解关于x的一元一次不等式:2x+b>mx+4.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△ABC沿x轴向左平移4个单位得到△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com