
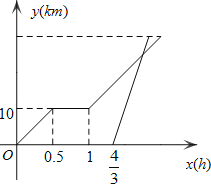
【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.
【答案】(1)![]() ,0.5h.(2)1.75,25km,(3)30km.
,0.5h.(2)1.75,25km,(3)30km.
【解析】
(1)根据图象可以求出小明在甲地游玩的时间,由速度=路程÷时间就可以求出小明骑车的速度;
(2)直接运用待定系数法就可以求出直线BC和DE的解析式,再由其解析式建立二元一次方程组,求出点F的坐标就可以求出结论;
(3)设从妈妈追上小明的地点到乙地的路程为n(km),根据妈妈比小明早到10分钟列出有关n的方程,求得n值即可.
(1)小明骑车速度:![]() ,
,
在甲地游玩的时间是1﹣0.5=0.5(h).
(2)妈妈驾车速度:20×3=60(km/h)
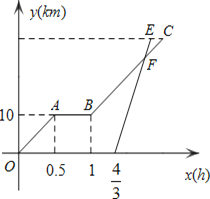
设直线BC解析式为y=20x+b1,
把点B(1,10)代入得b1=﹣10
∴y=20x﹣10
设直线DE解析式为y=60x+b2,把点D(![]() ,0)
,0)
代入得b2=﹣80∴y=60x﹣80…(5分)
∴![]()
解得![]()
∴交点F(1.75,25).
答:小明出发1.75小时(105分钟)被妈妈追上,此时离家25km.
(3)设从妈妈追上小明的地点到乙地的路程为n(km),
由题意得:![]()
∴n=5
∴从家到乙地的路程为5+25=30(km).


科目:初中数学 来源: 题型:
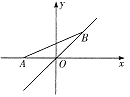
【题目】如图,点A的坐标为(-1,0),点B在直线![]() 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )
A. (0,0) B. (![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
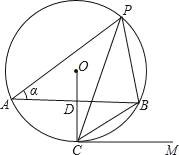
【题目】如图,AB是⊙O的弦,半径OC⊥AB交AB于点D,点P是⊙O上AB上方的一个动点(P不与A、B重合),已知∠APB=60°,∠OCB=2∠BCM.
(1)设∠A=α,当圆心O在∠APB内部时,写出α的取值范围;
(2)求证:CM是⊙O的切线;
(3)若OC=4,PB=4![]() ,求PC的长.
,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
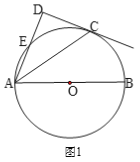
【题目】(1)如图1,点C在以AB为直径的⊙O上,AD与过点C的切线CD垂直,垂足为点D.
求证:AC平分∠DAB;
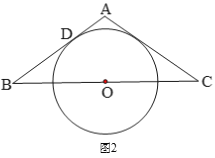
(2)如图2,△ABC为等腰三角形,AB=AC,O是BC的中点,AB与⊙O相切于点D.
求证:![]() 是⊙
是⊙![]() 的切线.
的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是规格为![]() 的正方形网格,请在所给网格中按下列要求操作:
的正方形网格,请在所给网格中按下列要求操作:
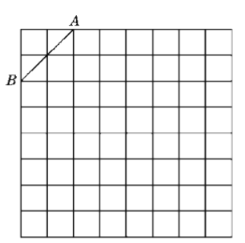
(1)请在网格中建立平面直角坐标系,使点A的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;
;
(2)在第二象限内的格点上找一点![]() ,使点
,使点![]() 与线段
与线段![]() 组成一个以
组成一个以![]() 为底的等腰三角形,且腰长是无理数,画出
为底的等腰三角形,且腰长是无理数,画出![]() ,则点
,则点![]() 的坐标是 ,
的坐标是 ,![]() 的周长是 (结果保留根号);
的周长是 (结果保留根号);
(3)作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
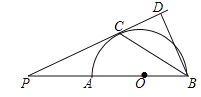
(1)∠PBC=∠CBD;
(2)![]() =ABBD.
=ABBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
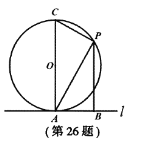
【题目】如图,直线![]() 与⊙
与⊙![]() 相切于点
相切于点![]() 为⊙
为⊙![]() 的直径,
的直径, ![]() 是直径
是直径![]() 右侧半圆上的一个动点(不与点
右侧半圆上的一个动点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]() .设
.设![]() ,
, ![]() .求: (1)
.求: (1)![]() 与
与![]() 相似吗?为什么?
相似吗?为什么?
(2)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() 取得最大值,最大值为多少?
取得最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为![]() (m2),种草所需费用
(m2),种草所需费用![]() 1(元)与
1(元)与![]() (m2)的函数关系式为
(m2)的函数关系式为 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用![]() 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).

(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与![]() 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com