
【题目】一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数关系如图中线段
之间的函数关系如图中线段![]() 所示;慢车离乙地的路程
所示;慢车离乙地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数关系如图中线段
之间的函数关系如图中线段![]() 所示,
所示,![]() 为线段
为线段![]() 、
、![]() 的交点.
的交点.
解读信息:
(1)甲、乙两地之间的距离为 ![]() ;
;
(2)点D的坐标为( ).
问题解决:
设快、慢车之间的距离为![]() ,求
,求![]() 与慢车行驶时间
与慢车行驶时间![]() 的函数关系式.
的函数关系式.
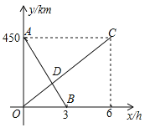
【答案】解读信息:(1)甲、乙两地之间的距离为450km;(2)点D的坐标为(2,150);问题解决:当0≤x≤2时,![]() ;当2<x≤3时,
;当2<x≤3时,![]() ;当3<x≤6时,
;当3<x≤6时,![]()
【解析】
(1)直接读图可得;
(2)分别求出AB、OC的函数解析式,联立得点D的坐标;
问题解决:分3段考虑,一段是两车相遇前,第二段是相遇后至快车到达终点前;第三段是快车已到达终点,慢车继续行驶直至到达终点.
(1)由图像可得,两地相距450km
(2)由图形可得:O(0,0),C(6,450),A(0,450),B(3,0)
可求得直线AB的解析式为:y=-150x+450
OC的解析式为:y=75x
联立两个方程得:-150x+450=75x
解得:x=2,y=150
∴D(2,150)
问题解决:
由AB、OC的解析式可知,快车的速度为150km/h,慢车的速度为75km/h
情况一:当0≤x≤2时,即快、慢两车相向而行
则y=450-(150+75)x,化简得:y=-225x+450
情况二:当2<x≤3时,即两车相遇后,分别继续向前行驶
y=(150+75)x-450,化简得:y=225x-450
情况三:当3<x≤6时,即快车已到达终点乙处,慢车还在继续行驶
y=75x


科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (k>0)与一次函数
(k>0)与一次函数![]() 的图象相交于两点A(
的图象相交于两点A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),线段AB交y轴与C,当|
),线段AB交y轴与C,当|![]() -
-![]() |=2且AC = 2BC时,k、b的值分别为( )
|=2且AC = 2BC时,k、b的值分别为( )

A. k=![]() ,b=2 B. k=
,b=2 B. k=![]() ,b=1 C. k=
,b=1 C. k=![]() ,b=
,b=![]() D. k=
D. k=![]() ,b=
,b=![]()
【答案】D
【解析】∵AC=2BC,∴A点的横坐标的绝对值是B点横坐标绝对值的两倍.∵点A、点B都在一次函数y=x+b的图象上,∴设B(m, ![]() m+b),则A(-2m,-m+b),∵|
m+b),则A(-2m,-m+b),∵|![]() -
-![]() |=2,∴m-(-2m)=2,解得m=
|=2,∴m-(-2m)=2,解得m=![]() ,又∵点A、点B都在反比例函数
,又∵点A、点B都在反比例函数![]() 的图象上,∴
的图象上,∴![]() (
(![]() +b)=(-
+b)=(-![]() )×(-
)×(-![]() +b),解得b=
+b),解得b=![]() ,∴k=
,∴k=![]() ×(
×(![]() +
+![]() )=
)=![]() ,故选D.
,故选D.
【题型】单选题
【结束】
11
【题目】若点(4,m)在反比例函数![]() (x≠0)的图象上,则m的值是 .
(x≠0)的图象上,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
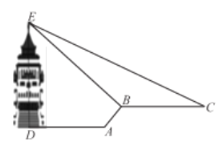
【题目】缙云山是国家级自然风景名胜区,上周周末,小明和妈妈到缙云山游玩,登上了香炉峰观景塔,从观景塔底中心![]() 处水平向前走
处水平向前走![]() 米到
米到![]() 点处,再沿着坡度为
点处,再沿着坡度为![]() 的斜坡
的斜坡![]() 走一段距离到达
走一段距离到达![]() 点,此时回望观景塔,更显气势宏伟,在
点,此时回望观景塔,更显气势宏伟,在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 再往前沿水平方向走
再往前沿水平方向走![]() 米到
米到![]() 处,观察到观景塔顶端的仰角是
处,观察到观景塔顶端的仰角是![]() ,则观景塔的高度
,则观景塔的高度![]() 为( )(tan22°≈0.4)
为( )(tan22°≈0.4)
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学不仅是一门学科,也是一种文化,即数学文化.数学文化包括数学史、数学美和数学应用等多方面.古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧.第![]() 格放
格放![]() 粒米,第
粒米,第![]() 格放
格放![]() 粒米,第
粒米,第![]() 格放
格放![]() 粒米,然后是
粒米,然后是![]() 粒、
粒、![]() 粒、
粒、![]() 粒······一只到第
粒······一只到第![]() 格.”“你真傻!就要这么一点米粒?”国王哈哈大笑.大臣说:“就怕您的国库里没有这么多米!”国王的国库里真没有这么多米吗?题中问题就是求
格.”“你真傻!就要这么一点米粒?”国王哈哈大笑.大臣说:“就怕您的国库里没有这么多米!”国王的国库里真没有这么多米吗?题中问题就是求![]() 是多少?请同学们阅读以下解答过程就知道答案了.
是多少?请同学们阅读以下解答过程就知道答案了.
设![]() ,
,
则![]()
![]()
![]()
即:![]()
事实上,按照这位大臣的要求,放满一个棋盘上的![]() 个格子需要
个格子需要![]() 粒米.那么
粒米.那么![]() 到底多大呢?借助计算机中的计算器进行计算,可知答案是一个
到底多大呢?借助计算机中的计算器进行计算,可知答案是一个![]() 位数:
位数:![]()
![]() ,这是一个非常大的数,所以国王是不能满足大臣的要求.请用你学到的方法解决以下问题:
,这是一个非常大的数,所以国王是不能满足大臣的要求.请用你学到的方法解决以下问题:
![]() 我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座
我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座![]() 层塔共挂了
层塔共挂了![]() 盏灯,且相邻两层中的下一层灯数是上一层灯数的
盏灯,且相邻两层中的下一层灯数是上一层灯数的![]() 倍,则塔的顶层共有多少盏灯?
倍,则塔的顶层共有多少盏灯?
![]() 计算:
计算: ![]()
![]() 某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:
某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:
已知一列数:![]() ,其中第一项是
,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,以此类推,求满足如下条件的所有正整数
,以此类推,求满足如下条件的所有正整数![]() ,且这一数列前
,且这一数列前![]() 项和为
项和为![]() 的正整数幂.请直接写出所有满足条件的软件激活码正整数
的正整数幂.请直接写出所有满足条件的软件激活码正整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
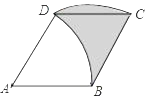
【题目】如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为( )
A. 2cm2B. 4![]() cm2C. 4cm2D. πcm2
cm2C. 4cm2D. πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
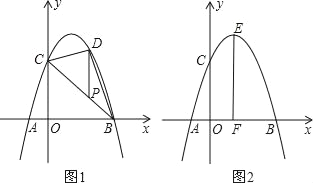
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
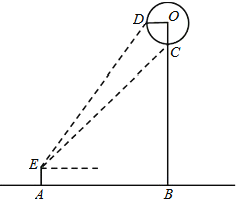
【题目】小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)
(参考数据:sin50°≈0.7660,cos50°≈0.6428,tan50°=1.192)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=![]() x+2的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数
x+2的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数![]() (x>0)的图象相交于C点.
(x>0)的图象相交于C点.
(1)写出A、B两点的坐标;
(2)作CD⊥x轴,垂足为D,如果OB是△ACD的中位线,求反比例函数![]() (x>0)的关系式.
(x>0)的关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com