
【题目】【问题引入】 已知:如图BE、CF是△ABC的中线,BE、CF相交于G.求证: ![]() =
= ![]() =
= ![]()

证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BC且EF= ![]() BC
BC
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
【思考解答】
(1)连结AG并延长AG交BC于H,点H是否为BC中点(填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是四边形. ②当 ![]() 的值为时,四边形EFMN 是矩形.
的值为时,四边形EFMN 是矩形.
③当 ![]() 的值为时,四边形EFMN 是菱形.
的值为时,四边形EFMN 是菱形.
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积S= .
【答案】
(1)是
(2)平行;1;![]() ;16
;16
【解析】解:(1)如图,连结EF,交AG于O, 
∵E、F分别是AC、AB的中点,
∴EF是△ABC的中位线,
∴EF∥BC且EF= ![]() BC,
BC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∵OE∥BH,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵OE∥CH,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BH=CH,即点H是BC中点;
所以答案是:是;
·(2)①∵M、N分别是GB、GC的中点,
∴MN是△GBC的中位线,
∴MN∥BC且MN= ![]() BC,
BC,
由(1)可得,EF∥BC且EF= ![]() BC,
BC,
∴EF∥MN,EF=MN,
∴四边形EFMN是平行四边形,
所以答案是:平行;
②当四边形EFMN是矩形时,FG=EG,
∵ ![]() =
= ![]() =
= ![]() ,
,
∴GB=GC,
∴∠GBC=∠GCB,
又∵H是BC的中点,
∴GH⊥BC,即AH⊥BC,
∴AH垂直平分BC,
∴AB=AC,
∴ ![]() 的值为1,
的值为1,
所以答案是:1;
③当四边形EFMN是菱形时,MN=FM,
∵MN是△BCG的中位线,
∴MN= ![]() BC,
BC,
∵FM是△ABG的中位线,
∴FM= ![]() AG,
AG,
又∵G是△ABC的重心,
∴AG= ![]() AH,
AH,
∴FM= ![]() AG=
AG= ![]() AH,
AH,
∴ ![]() BC=
BC= ![]() AH,即2BC=3AH,
AH,即2BC=3AH,
∴ ![]() 的值为
的值为 ![]() ,
,
所以答案是: ![]() ;
;
④当AB=AC时,由②可得四边形EFMN是矩形,AH⊥BC,
∵AB=10,BC=16,
∴BH= ![]() BC=8,AH=6,
BC=8,AH=6,
∵MN是△BCG的中位线,
∴MN= ![]() BC=8,
BC=8,
∵FM是△ABG的中位线,
∴FM= ![]() AG=
AG= ![]() AH=2,
AH=2,
∴矩形EFMN的面积S=FM×MN=2×8=16,
所以答案是:16.
【考点精析】掌握三角形中位线定理和平行线分线段成比例是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;三条平行线截两条直线,所得的对应线段成比例.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小明按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
(1)若小明任意按下一个开关,则下列说法正确的是( )
A.小明打开的一定是楼梯灯;
B.小明打开的可能是卧室灯;
C.小明打开的不可能是客厅灯;
D.小明打开走廊灯的概率是 ![]()
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,国务院连续发布了《关于加快构建大众创业万众创新支撑平台的指导意见》等一系列支持性政策,各地政府高度重视、积极响应,中国掀起了大众创业万众创新的新浪潮.某创新公司生产营销A、B两种新产品,根据市场调研,发现如下信息: 信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系y=ax2+bx,当x=1时,y=7;当x=2时,y=12.
信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系y=2x.
根据以上信息,解答下列问题:
(1)求a,b的值;
(2)该公司准备生产营销A、B两种产品共10吨,请设计一个生产方案,使销售A、B两种产品获得的利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解学生参加体育活动的情况,对学生“平均每天参加体育活动的时间”进行了随机抽样调查,下图是根据调查结果绘制的两幅不完整的统计图. 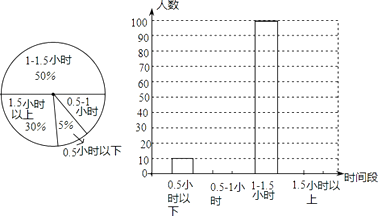
请你根据统计图提供的信息,解答以下问题:
(1)“平均每天参加体育活动的时间”“为0.5~1小时”部分的扇形统计图的圆心角为度;
(2)本次一共调查了名学生;
(3)将条形统计图补充完整;
(4)若该校有2000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com